cho tam giác ABC có AB = AC .M là trung điểm của BC a, Chứng minh tam giác AMB = tam giác AMC .b, Từ M kẻ MA vuông góc với AB , MF vuông góc với AC.chứng minh AE=AFc, Chứng minh EF//BC d, Từ B kẻ đường thẳng vuông góc với AB ,từ C kẻ đường thẳng vuông góc với AC, hai đường thẳng này cắt nhau ở N. Chứng minh 3 điểm A,M,N thẳng...
Đọc tiếp
cho tam giác ABC có AB = AC .M là trung điểm của BC
a, Chứng minh tam giác AMB = tam giác AMC .
b, Từ M kẻ MA vuông góc với AB , MF vuông góc với AC.chứng minh AE=AF
c, Chứng minh EF//BC
d, Từ B kẻ đường thẳng vuông góc với AB ,từ C kẻ đường thẳng vuông góc với AC, hai đường thẳng này cắt nhau ở N. Chứng minh 3 điểm A,M,N thẳng hàng
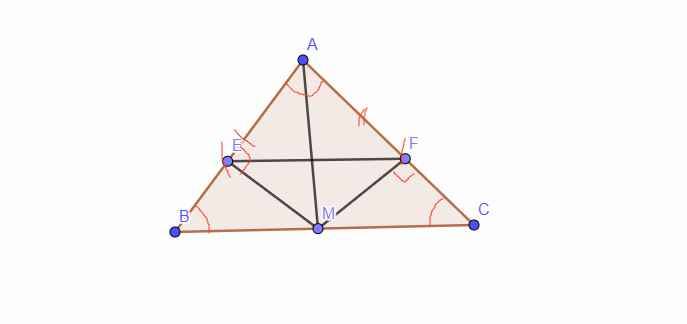
Sửa câu b: Từ M kẻ ME
Bg
a/ Xét hai tam giác AMB và AMC có:
AB = AC (gt)
BM = MC (vì M là trung điểm của BC)
AM là cạnh chung
Nên \(\Delta AMB=\Delta AMC\)(c.c.c)
Vậy \(\Delta AMB=\Delta AMC\)
b/ Xét hai tam giác vuông AME và AMF có:
\(\widehat{EAM}=\widehat{FAM}\)(vì \(\Delta AMB=\Delta AMC\))
AM là cạnh chung
Nên \(\Delta AME=\Delta AMF\)(g.c.g)
Do đó AE = AF (hai cạnh tương ứng)
Vậy AE = AF
c và d hơi dài. Đợi một thời gian :((
một thời gian là bao lâu vậy bạn ?