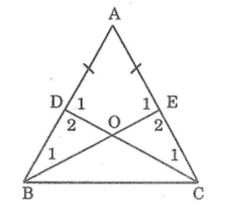
cho tam giác ABC có AB = AC. Lấy điểm D trên cạnh AB, lấy điểm E trên cạnh AC sao cho AD=AE
a) Chứng minh : BE = CD
b) Gọi O là giao điểm của BE và CD. Chứng minh rằng ΔBOD = ΔCOE
c) Chứng minh: AO là tia phân giác của góc BAC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
31 tháng 3 2018
ΔBEA= ΔCDA (chứng minh trên)
⇒∠(B1 ) =∠(C1 ) ;∠(E1 ) =∠(D1 ) (hai góc tương ứng) (1)
+) Ta có: ∠(E1 ) +∠(E2 ) =180o (hai góc kề bù) (2)
Và ∠(D1 ) +∠(D2 ) =180o (hai góc kề bù) (3)
Từ (1); (2) và (3) suy ra: ∠(E2 ) =∠(D2 )
+) Theo giả thiết ta có; AB = AC
Và AD = AE
Lấy vế trừ vế, suy ra:
AB - AD = AC - AE hay BD = CE
Xét ΔOEC và ΔOCE, ta có:
∠(D2 ) =∠(E2 ) (chứng minh trên)
DB=EC (chứng minh trên)
∠(B1 ) =∠(C1 ) (chứng minh trên)
Suy ra: ΔODB= ΔOCE ( g.c.g)
26 tháng 12 2021
a: Xét ΔABE và ΔACD có
AB=AC
\(\stackrel\frown{A}\) chung
AE=AD
Do đó: ΔABE=ΔACD
Suy ra: BE=CD
28 tháng 1 2022
a: Xét ΔABE và ΔACD có
AB=AC
\(\widehat{BAE}\) chung
AE=AD
Do đó: ΔABE=ΔACD
b: Xét ΔDBC và ΔECB có
DB=EC
\(\widehat{DBC}=\widehat{ECB}\)
BC chung
Do đó: ΔDBC=ΔECB
Xét ΔBOD và ΔCOE có
\(\widehat{ODB}=\widehat{OEC}\)
DB=EC
\(\widehat{DBO}=\widehat{ECO}\)
Do đó: ΔBOD=ΔCOE
19 tháng 8 2016
a/ Xét 2 tam giác BDE và CED có
BD=EC
DE chung
Góc BDE = góc DEC do chúng lần lượt bù với 2 góc bằng nhau là ADE và AED
=> dpcm (c.g.c)
b/ Có góc DKB bằng góc EKC do đối đỉnh
KD=KE
góc BDK=góc CEK
Vậy tam giác BOD = tam giác COE
19 tháng 8 2016
a/ Xét tam giác ABE và tam giác ACD có :
AD = AE , góc A là góc chung của hai tam giác , AB = AC
=> tam giác ABE = tam giác ACD => CD = BE
b/ Dễ dàng chứng minh đc tam giác BED = tam giác CDE (c.c.c)
=> góc CED = góc CDE => tam giác ODE cân tại O => OD = OE (1)
Lại có BE = CD => OB = OC (2) ; góc BOD = góc EOC (đối đỉnh) (3)
Từ (1) , (2) , (3) suy ra tam giác BOD = tam giác OCE (c.g.c)
19 tháng 8 2016
a) Xét tam giác ABE và tam giác ACD:
có+AB=AC(gt)
+A: góc chung
+AD=AE(gt)
Vậy tam giác ABE=tam giác ACD(c.g.c)
=> BE=CD( 2 cạnh tương ứng )
b)
- Vì tam giác ABE=tam giác ACD(cmt)
nên: ABD=ACE( 2 góc tương ứng )
- Xét tam giác BOD và tam giác COE:
có:+ góc BOD=COE( đối đỉnh)
+AB=AC( tam giác ABC cân vì có 2 cạnh bên bằng nhau) mà AD=AE(gt)=>BD=CE
+góc ABE=ACD(cmt)
Vậy tam giác BOD=COE(g.c.g)
^...^ 
^_^
10 tháng 7 2019
Cm: a) Xét t/giác ABE và t/giác ACD
có: AB = AC (gt)
\(\widehat{A}\) :chung
AE = AD (gt)
=> t/giác ABE = t/giác ACD (c.g.c)
=> BE = CD (2 cạnh t/ứng)
b)Ta có: AD + DB = AB
AE + EC = AC
mà AD = AE (gt) ; AB = AC (gt)
=> BD = EC
Ta lại có: \(\widehat{ADC}+\widehat{CDB}=180^0\) (kề bù)
\(\widehat{AEB}+\widehat{BEC}=180^0\)(kề bù)
mà \(\widehat{ADC}=\widehat{AEB}\)(vì t/giác ABE = t/giác ACD)
=> \(\widehat{BDC}=\widehat{BEC}\)
Xét t/giác BOD và t/giác COE
có: \(\widehat{DBO}=\widehat{OCE}\) (vì t/giác ABE = t/giác ACD)
BD = EC (cmt)
\(\widehat{BDO}=\widehat{OEC}\) (cmt)
=> t/giác BOD = t/giác COE (g.c.g)
c) Xét t/giác ABO và t/giác ACO
có: AB = AC (gT)
OB = OC (vì t/giác BOD = t/giác COE)
AO : chung
=> t/giác ABO = t/giác ACO (c.c.c)
=> \(\widehat{BAO}=\widehat{CAO}\) (2 góc t/ứng)
=> AO là tia p/giác của \(\widehat{A}\)
d) Xét t/giác ABH và t/giác ACH
có: AB = AC (gt)
\(\widehat{BAH}=\widehat{CAH}\)(cmt)
AH : chung
=> t/giác ABH = t/giác ACH (c.g.c)
=> \(\widehat{BHA}=\widehat{CHA}\) (2 góc t/ứng)
Mà \(\widehat{BHA}+\widehat{CHA}=180^0\) (kề bù)
=> \(\widehat{BHA}=\widehat{CHA}=90^0\) => AH \(\perp\)BC (Đpcm)
11 tháng 8 2021
a: Xét ΔAEB và ΔADC có
AE=AD
\(\widehat{DAC}\) chung
AB=AC
Do đó: ΔAEB=ΔADC
Suy ra: BE=CF
b: Ta có: AD+DB=AB
AE+EC=AC
mà AD=AE
và AB=AC
nên DB=EC
Xét ΔDBC và ΔECB có
DB=EC
\(\widehat{DBC}=\widehat{ECB}\)
BC chung
Do đó: ΔDBC=ΔECB
Suy ra: \(\widehat{ODB}=\widehat{OEC}\)
Xét ΔODB và ΔOEC có
\(\widehat{ODB}=\widehat{OEC}\)
BD=EC
\(\widehat{DBO}=\widehat{ECO}\)
Do đó: ΔODB=ΔOEC
