Tính bằng cách thuận tiện nhất: (1+1/2+1/4+1/8+1/16)/(1-1/2+1/4-1/8+1/16)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




1/2+1/4+1/8+1/16+1/32+1/64
=(1/2+1/4+1/8)+(1/16+1/32+1/64)
=(4/8+2/8+1/8)+(4/64+2/64+1/64)
=7/8+7/64
=56/64+7/64
=63/64
B = \(\dfrac{1}{2}\) + \(\dfrac{1}{4}\) + \(\dfrac{1}{8}\) + \(\dfrac{1}{16}\) + \(\dfrac{1}{32}\) + \(\dfrac{1}{64}\)
2 x B = 1 + \(\dfrac{1}{2}\)+ \(\dfrac{1}{4}\) + \(\dfrac{1}{8}\) + \(\dfrac{1}{16}\)+ \(\dfrac{1}{32}\)
2 x B - B = 1 - \(\dfrac{1}{64}\)
B = \(\dfrac{63}{64}\)

voi lai phan so sau hon phan so truoc la 2 doi vi anh nhat linh a?


\(\dfrac{1}{4}:0,25-\dfrac{1}{8}:0,125+\dfrac{1}{2}:0,5-\dfrac{1}{16}:0,0625\\ =0,25:0,25-0,125:0,125+0,5:0,5-0,0625:0,0625\\ =1-1+1-1\\ =0+1-1\\ =1-1\\ =0\)

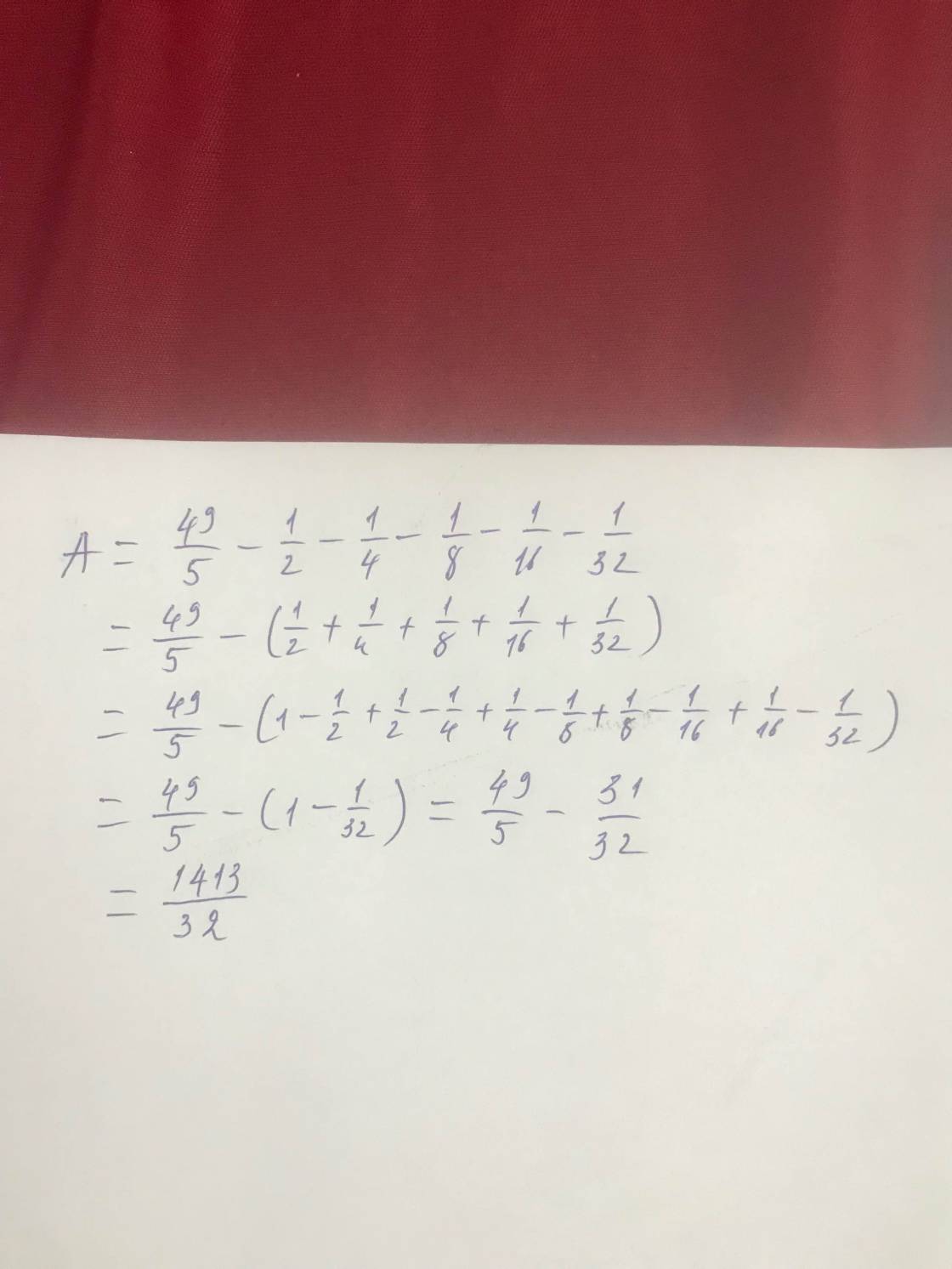
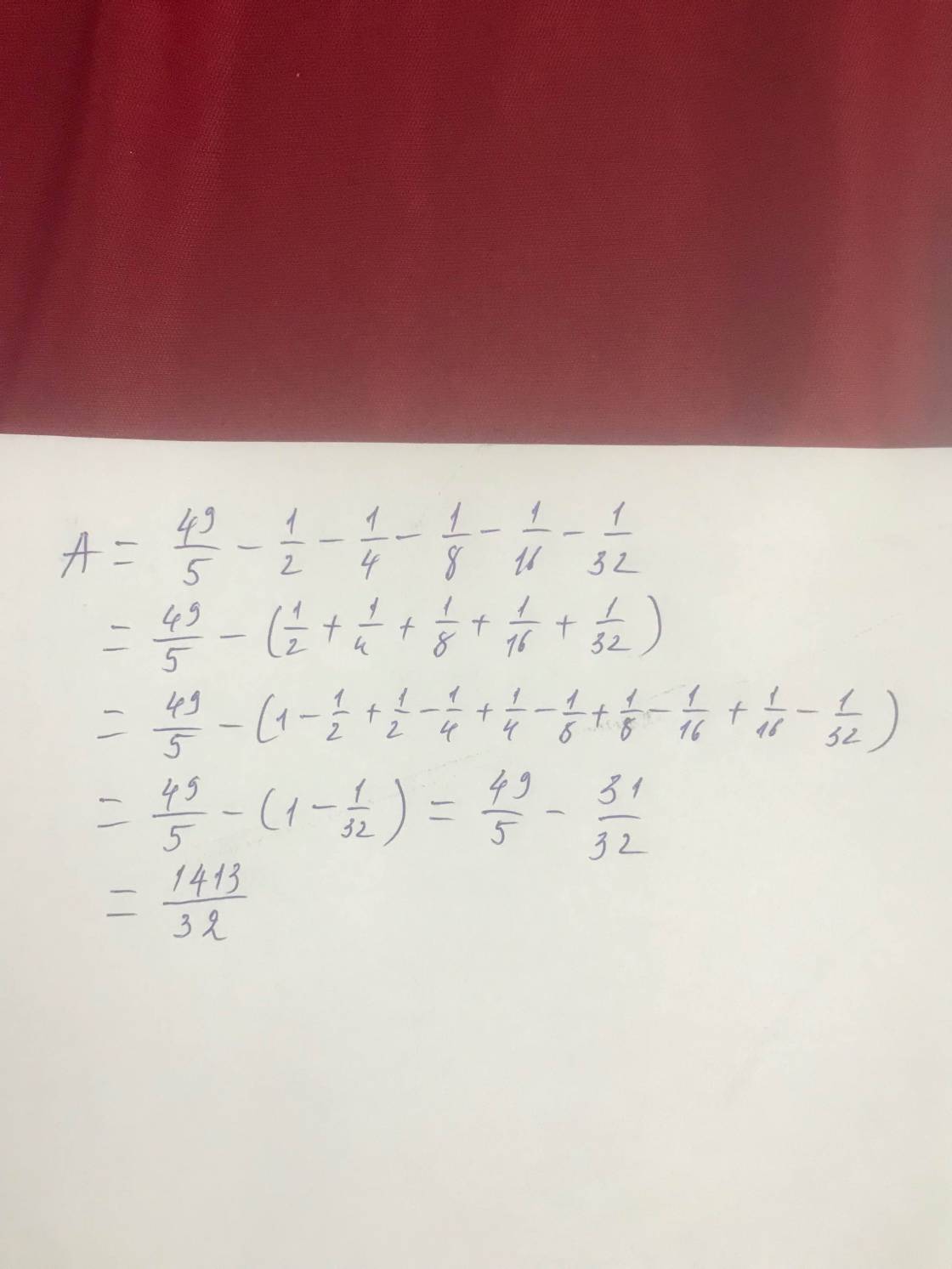
Bài làm
\(\frac{\left(1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}\right)}{\left(1-\frac{1}{2}+\frac{1}{4}-\frac{1}{8}+\frac{1}{16}\right)}\)
\(=\frac{\left(\frac{2}{2}+\frac{1}{2}+\frac{1}{2^2}+\frac{1}{2^3}+\frac{1}{2^4}\right)}{\left(\frac{2}{2}-\frac{1}{2}+\frac{1}{2^2}-\frac{1}{2^3}+\frac{1}{2^4}\right)}\)
\(=\frac{\frac{1}{2}\left(2+1+\frac{1}{2}+\frac{1}{2^2}+\frac{1}{2^3}\right)}{\frac{1}{2}\left(2-1+\frac{1}{2}-\frac{1}{2^2}+\frac{1}{2^3}\right)}\)
\(=\frac{3+\frac{1}{2}+\frac{1}{2^2}+\frac{1}{2^3}}{1+\frac{1}{2}-\frac{1}{2^2}+\frac{1}{2^3}}\)
\(=\frac{\frac{24}{8}+\frac{4}{8}+\frac{2}{8}+\frac{1}{8}}{\frac{8}{8}+\frac{4}{8}-\frac{2}{8}+\frac{1}{8}}\)
\(=\frac{31}{8}\div\frac{11}{8}\)
\(=\frac{31}{8}\cdot\frac{8}{11}\)
\(=\frac{31}{11}\)
P/S: Trông không thuận tiện lắm :/
Hawy tính giúp mình nha mình cho đúng