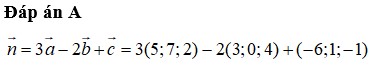Bài 11: Cho 3 điểm A(1,2), B(-2, 6), C(4, 4). i) Hãy phân tích AB, theo 2 véc tơ AU và CB ; theo 2 véctơ AC và CN
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án:
AD+BC
=ED-EA+EC-EB
=(ED+EC)-(EA+EB) (1)
Mà E là trung điểm của AB=> EA+EB=0
(1)=2EF (F là trung điểm DC)

a) \(\overrightarrow{PM}=\overrightarrow{PB}+\overrightarrow{BM}=\frac{1}{2}\overrightarrow{AB}+2\left(\overrightarrow{AC}-\overrightarrow{AB}\right)=2\overrightarrow{AC}-\frac{3}{2}\overrightarrow{AB}\)
Do \(\overrightarrow{NA}+2\overrightarrow{NC}=\overrightarrow{0}\)nên N thuộc đoạn AC và \(\overrightarrow{AN}=\frac{2}{3}\overrightarrow{AC}\)
\(\overrightarrow{PN}=\overrightarrow{PA}+\overrightarrow{AN}=-\frac{1}{2}\overrightarrow{AB}+\frac{2}{3}\overrightarrow{AC}=\frac{2}{3}\overrightarrow{AC}-\frac{1}{2}\overrightarrow{AB}\)
b) Ta thấy \(\overrightarrow{PN}=\frac{1}{3}\left(2\overrightarrow{AC}-\frac{3}{2}\overrightarrow{AB}\right)=\frac{1}{3}\overrightarrow{PM}\). Suy ra M,N,P thẳng hàng (đpcm).

\(\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CD}+\overrightarrow{DA}\)
\(=\overrightarrow{AC}+\overrightarrow{CA}\)
\(=\overrightarrow{0}\)

1) Các vecto bằng vecto EF là:
\(\overrightarrow{EF}=\overrightarrow{DO}=\overrightarrow{OA}=\overrightarrow{CB}\)

a: \(\Leftrightarrow\left\{{}\begin{matrix}2x-3y=-4\\-x+4y=7\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x-3y=-4\\-2x+8y=14\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}5y=10\\-x+4y=7\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=2\\x=1\end{matrix}\right.\)
Vậy: \(\overrightarrow{C}=\overrightarrow{a}+2\overrightarrow{b}\)