Cho phương trình x 2 - 2x + m = 0 (1) Với giá trị nào của m thì phương trình (1)
Có nghiệm?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
Cho phương trình x 2 - 2x + m = 0 (1) Với giá trị nào của m thì phương trình (1)
Có hai nghiệm dương?
1
CM
17 tháng 7 2017
x 2 - 2x + m = 0 (1)
∆ ' = - 1 2 - 1.m = 1 - m
Để phương trình (1) có hai nghiệm dương thì:
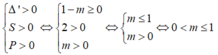
Vậy với 0 < m ≤ 1 thì phương trình (1) có hai nghiệm dương
CM
2 tháng 1 2019
x 2 - 2x + m = 0 (1)
∆ ' = - 1 2 - 1.m = 1 - m
Để phương trình có hai nghiệm trái dấu thì:
P < 0 ⇔ m < 0
Vậy với m < 0 thì phương trình (1) có hai nghiệm trái dấu
CM
6 tháng 11 2017
Ta có: a = 7, b= 2(m-1), c = - m2
Suy ra: Δ' = (m - 1)2 + 7m2
Do (m-1)2 ≥ 0 mọi m và m2 ≥ 0 mọi m
=> ∆’≥ 0 với mọi giá trị của m.
Do đó phương trình có nghiệm với mọi giá trị của m.
4 tháng 2 2022
a: Ta có: \(\left(m-1\right)x^2-2x-m+1=0\)
a=m-1; b=-2; c=-m+1
\(ac=\left(m-1\right)\left(-m+1\right)=-\left(m-1\right)^2< 0\forall m\)
Do đó: Phương trình luôn có hai nghiệm trái dấu
b: \(x_1^2+x_2^2=6\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=6\)
\(\Leftrightarrow\left(\dfrac{2}{m-1}\right)^2-2\cdot\dfrac{-m+1}{m-1}=6\)
\(\Leftrightarrow\dfrac{4}{\left(m-1\right)^2}=4\)
\(\Leftrightarrow\left(m-1\right)^2=1\)
=>m-1=1 hoặc m-1=-1
=>m=2 hoặc m=0
CM
20 tháng 7 2018
Phương trình có nghiệm kép khi m ≠ -2 và Δ = 0.
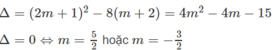
Khi m = 5/2 nghiệm kép của phương trình là
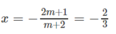
Khi m = -3/2 nghiệm kép của phương trình là x = 2.
CM
3 tháng 1 2020
Phương trình (1):
+ Vô nghiệm ⇔ Δ’ < 0 ⇔ 1 – 2m < 0 ⇔ 2m > 1 ⇔ m >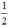 
+ Có nghiệm kép ⇔ Δ’ = 0 ⇔ 1 – 2m = 0 ⇔ m =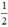 
+ Có hai nghiệm phân biệt ⇔ Δ’ > 0 ⇔ 1 – 2m > 0 ⇔ 2m < 1 ⇔ m <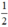 
Vậy: Phương trình (1) có hai nghiệm phân biệt khi m <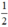 
; có nghiệm kép khi m = 
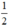và vô nghiệm khi m >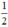 
x 2 - 2x + m = 0 (1)
∆ ' = - 1 2 - 1.m = 1 - m
Để phương trình (1) có nghiệm thì:
∆ ' ≥ 0 ⇔ 1 - m ≥ 0 ⇔ m ≤ 1
Vậy với m ≤ 1 thì phương trình (1) có nghiệm.