Đèn : 140V - 490W
R1 = 30 ôm
Rb = 20 ôm
U = 250 không đổi
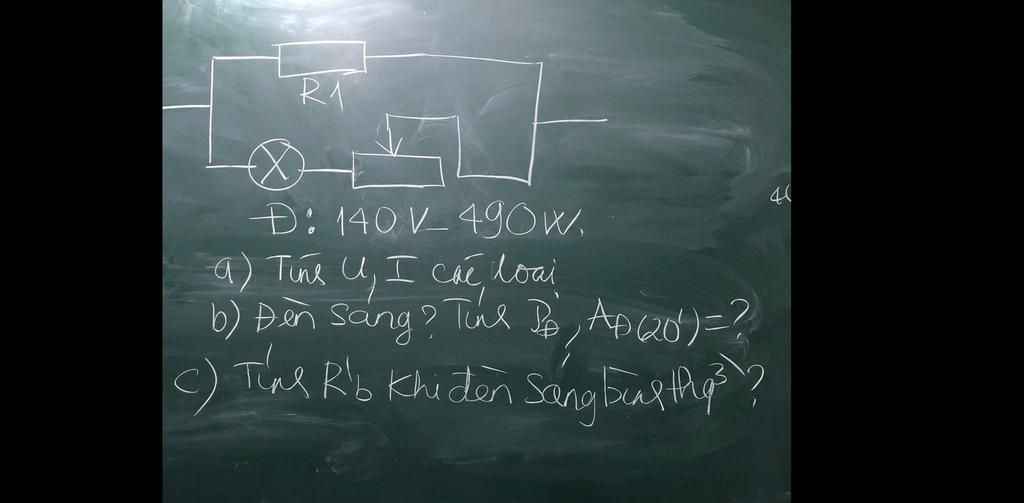
LÀM GẤP GIÚP MÌNH VỚI Ạ MÌNH CẦN GẤP LẮM
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
2
giúp mình với ạ, mình cần gấp lắm ạ
29 tháng 12 2021
a: Xét tứ giác ABDC có
M là trung điểm của BC
M là trung điểm của AD
Do đó: ABDC là hình bình hành
mà \(\widehat{BAC}=90^0\)
nên ABDC là hình chữ nhật
LA
Giúp mình với ạ, mình cần gấp lắm ạ!
1
AH
Akai Haruma
Giáo viên
7 tháng 8 2021
Lời giải:
Đặt \(\sqrt[3]{5\sqrt{2}+7}=m; \sqrt[3]{5\sqrt{2}-7}=n\)
\(m^3-n^3=14\)
\(mn=1\)
\((a+b+c)^3=(m-n)^3=m^3-3mn(m-n)-n^3=14-3(m-n)\)
\(\Leftrightarrow (a+b+c)^3=14-3(a+b+c)\)
\(\Leftrightarrow (a+b+c)^3+3(a+b+c)-14=0\)
\(\Leftrightarrow (a+b+c)^2[(a+b+c)-2]+2(a+b+c)(a+b+c-2)+7(a+b+c-2)=0\)
\(\Leftrightarrow (a+b+c-2)[(a+b+c)^2+2(a+b+c)+7]=0\)
Dễ thấy biểu thức trong ngoặc vuông $>0$ nên $a+b+c-2=0$
$\Leftrightarrow a+b+c=2$
$ab+bc+ac=\frac{(a+b+c)^2-(a^2+b^2+c^2)}{2}=\frac{2^2-1}{2}=\frac{3}{2}$
3 tháng 7 2023
5:
a: Xét ΔABD vuông tại D và ΔACE vuông tại E có
góc A chung
=>ΔABD đồng dạng với ΔACE
b; ΔABD đồng dạng với ΔACE
=>AD/AE=AB/AC
=>AD/AB=AE/AC
Xét ΔADE và ΔABC có
AD/AB=AE/AC
góc DAE chung
=>ΔADE đồng dạng với ΔABC
c: ΔADE đồng dạng với ΔABC
=>S ADE/S ABC=(AD/AB)^2=1/4
DT
Đỗ Thanh Hải
CTVVIP
12 tháng 9 2021
1 Jill reminded John to do the washing up
2 The police ordered his men to search all the shops on that street
3 She blamed me for ignoring the notice about life-saving equipment
4 My aunt advised me not to argut with my father
5 Stella congratulated Jeff on having got an promotion at last
6 Kevin apoligized to Sarah for making her angry
7 The man warn his son to put down the gun
8 Ron denied being in the town on the night of the robbery
9 Ted promise to pay back the money at the end of that month
10 George encouraged Susan to send her story to the magazine
11 Natalie accused Tom of lying to her
MCD: \(R1//\left(R2ntR3\right)\)
\(\Rightarrow U=U1=U23=250V\)
\(\Rightarrow\left\{{}\begin{matrix}U3=140V\\U2=U23-U3=250-140=110V\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}I1=U1:R1=250:30=\dfrac{25}{3}A\\I2=U2:R2=110:20=\dfrac{11}{2}A\\I3=I2=\dfrac{11}{2}A\left(R1ntR3\right)\end{matrix}\right.\)
\(U_Đ=140V;I_Đ=\dfrac{P_Đ}{U_Đ}=\dfrac{490}{140}=3,5A\)
\(R_Đ=\dfrac{U^2_Đ}{P_Đ}=\dfrac{140^2}{490}=40\Omega\)
\(R_2=R_{Đ+b}=R_Đ+R_b=40+20=60\Omega\)
\(R_{tđ}=\dfrac{R_1\cdot R_2}{R_1+R_2}=\dfrac{30\cdot60}{30+60}=20\Omega\)
\(U_1=U_m=250V\)
\(I_1=\dfrac{U_1}{R_1}=\dfrac{250}{30}=\dfrac{25}{3}A\)
\(I_2=\dfrac{U}{R_2}=\dfrac{250}{60}=\dfrac{25}{6}A\)\(\Rightarrow I_Đ=I_b=\dfrac{25}{6}A\)