Cho sinα = -2 5 /5 với 3π/2 < α < 2π. Giá trị cotα là
A. 1/2 B. 1/ 5
C. -1/2 D. -3/ 5
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Vì tanα = 2cotα và 3π/2 < α < 2π nên 3π/2 < α < 7π/4.
Do đó sinα < (- 2 )/2 và cosα < 2 /2.
Vì vậy sinα + cosα < 0.
Suy ra các phương án A, C, D bị loại.
Đáp án: B

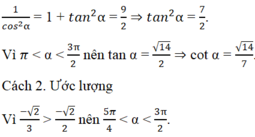
Suy ra 0 < cot α < 1. Vậy các phương án A, B, C bị loại.
Đáp án: D

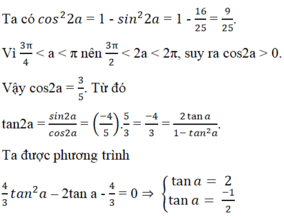
Vì 3π/4 < a < π nên tan a < 0. Vậy tan a = (-1)/2. Đáp án là D.

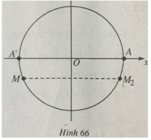
(h.66) Ta có
A M 2 = MA’ = MA + AA’
Suy ra
Sđ A M 2 = -α + π + k2π, k ∈ Z.
Vậy đáp án là B.
6.13. (h.67) Ta có
Sđ A M 3 = -sđ AM = -α + k2π, k ∈ Z.
Đáp án: D

\(1-2cos^2x-sinx=0\)
\(\Leftrightarrow1-2\left(1-sin^2x\right)-sinx=0\)
\(\Leftrightarrow2sin^2x-sinx-1=0\Rightarrow\left[{}\begin{matrix}sinx=1\\sinx=-\dfrac{1}{2}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{2}+k2\pi\\x=-\dfrac{\pi}{6}+k2\pi\\x=\dfrac{7\pi}{6}+k2\pi\end{matrix}\right.\)
\(\Rightarrow x=\left\{\dfrac{\pi}{2};\dfrac{7\pi}{6};\dfrac{11\pi}{6};\dfrac{5\pi}{2}\right\}\)
\(\Rightarrow\sum x=6\pi\)

a: Để A là số nguyên thì 3pi-1 thuộc Ư(12)
=>3pi-1 thuộc {1;-1;2;-2;3;-3;4;-4;6;-6;12;-12}
mà pi là số nguyên
nên pi thuộc {0;1;-1}
b: Để B là số nguyên thì
2pi-6+11 chia hết cho pi-3
=>pi-3 thuộc {1;-1;11;-11}
=>pi thuộc {4;2;14;-8}
c o t 2 α = 1 / ( sin 2 α ) – 1 = 25 / 20 – 1 = 1/4 ⇒ cotα = ±1/2.
Vì 3π/2 < α < 2π nên cotα < 0. Vậy cotα = (-1)/2.
Đáp án: C