Cho tanα + cotα = -2. Giá trị của biểu thức N = tan 3 α + c o t 3 α là
A. 3 B. 4
C. -2 D. 2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vì \(\dfrac{\pi}{2}< \alpha< \pi\) \(\Rightarrow\) cos \(\alpha\) < 0
\(\Rightarrow\) cos \(\alpha\) = \(-\sqrt{1-sin^2\alpha}\) = \(-\dfrac{2\sqrt{2}}{3}\)
\(\Rightarrow\) tan \(\alpha\) = \(\dfrac{sin\alpha}{cos\alpha}=\dfrac{-\sqrt{2}}{4}\)
\(\Rightarrow\) cot \(\alpha\) = \(\dfrac{1}{tan\alpha}\) = \(-2\sqrt{2}\)
Chúc bn học tốt!

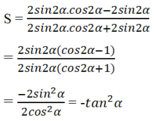
Đáp án: A
Ta cũng có thể suy luận cos2α – 1 < 0, cos2α + 1 > 0 nên S < 0, do đó các phương án B, C, D bị loại. Vậy đáp án là A.

Chọn C.
Nhân cả tử và mẫu với tanα và chú ý tanα.cotα = 1 ta được:

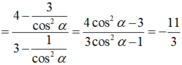

c o t 2 α = 1 / ( sin 2 α ) – 1 = 25 / 20 – 1 = 1/4 ⇒ cotα = ±1/2.
Vì 3π/2 < α < 2π nên cotα < 0. Vậy cotα = (-1)/2.
Đáp án: C

Đặt \(\tan\alpha=a;\cot\alpha=b\)
Theo đề, ta có: \(\left(a+b\right)^2-\left(a-b\right)^2\)
\(=a^2+2ab+b^2-a^2+2ab-b^2\)
\(=4ab=4\cdot\tan\alpha\cdot\cot\alpha=4\)

Chọn C.
Ta có tan α – cotα = 1

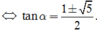
Do ![]() suy ra tanα < 0 nên
suy ra tanα < 0 nên
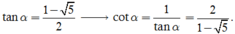
Thay
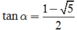 và
và 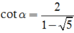
vào P ta được
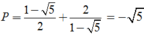
Ta có tanα + cotα = tanα + 1/tanα.
Do đó tanα + cotα ≤ -2 hoặc tanα + cotα ≥ 2.
Dấu “=” xảy ra khi tanα = cotα = -1 hoặc tanα = cotα = 1.
Với giả thiết tanα + cotα = -2 thì tanα = cotα = -1.
Do đó N = tan 3 α + c o t 3 α = -2
Đáp án là C.