Cho góc xOy khác góc bẹt, điểm A thuộc cạnh Ox, điểm B thuộc cạnh Oy. Hãy tìm điểm M nằm trong góc xOy và cách đều hai cạnh Ox và Oy nên M thuộc tia phân giác Oz của ∠(xOy); cách đều Ox, Oy và cách đều A, B.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


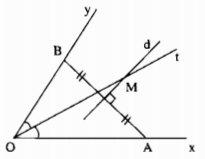
a) - Điểm nằm trong góc xOy và cách đều hai cạnh Ox và Oy nên nó thuộc tia phân giác Ot của góc xOy
- Điểm cách đều 2 điểm A và B thuộc đường thẳng d là đường trung trực của AB
Vậy M là giao điểm của dường trung trực của đoạn thẳng AB và tia phân giác Ot của góc xOy
b) Nếu OA = OB
⇒ ∆OAB cân tại O
Tia phân giác của góc xOy cũng là đường trung trực của AB. Vậy bất kỳ điểm M nào nằm trên tia phân giác của góc xOy đều thỏa mãn điều kiện câu a.

a.
Xét tam giác AHO vuông tại A và tam giác BHO vuông tại B có:
AOH = BOH (OH là tia phân giác của AOB)
OH là cạnh chung
=> Tam giác AHO = Tam giác BHO (cạnh huyền - góc nhọn)
=> AH = BH (2 cạnh tương ứng)
=> Tam giác HAB cân tại H
b.
OA = OB (tam giác AHO = tam giác BHO)
=> Tam giác OAB cân tại O
OH là tia phân giác của tam giác OBA cân tại O
=> OH là đường cao của tam giác OBA
mà AD là đường cao của tam giác OAB
=> C là trực tâm của tam giác OAB
=> BC là đường cao của tam giác OAB
=> BC _I_ Ox
Chúc bạn học tốt![]()
Phương An làm 2 câu a,b giờ tớ làm câu c luôn nhé ;)
Ta thấy tam giác HAO là tam giác có 1 góc là 30 độ nên HO=2OA = > OA =2 (cm)
Dựa vào tính chất trong 1 tam giác có 1 góc là 30 độ thì cạnh huyền gấp 2 lần cạnh đối diện với góc 30 độ

Tìm M khi độ dài đoạn OA, OB là bất kì
- Vì M cách đều hai cạnh Ox, Oy của góc xOy nên M nằm trên đường phân giác Oz của góc xOy (1).
- Vì M cách đều hai điểm A, B nên M nằm trên đường trung trực của đoạn AB (2).
Từ (1) và (2) ta xác định được điểm M là giao điểm của đường phân giác Oz của góc xOy và đường trung trực của đoạn AB.

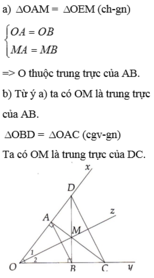
Vì điểm M nằm trong góc xOy và cách đều hai cạnh Ox và Oy nên M thuộc tia phân giác Oz của ∠(xOy).
Vì điểm M cách đều 2 điểm A và B nên M thuộc đường trung trực của AB.
Vậy M là giao điểm của đường trung trực của đoạn thẳng AB và tia phân giác Oz của ∠(xOy)
Do đó, có vô số điểm M thỏa mãn điều kiện trong câu a) khi OA = OB.