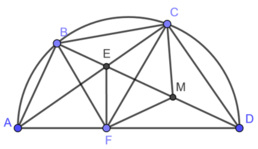
cho tứ giác ABCd nội tiếp đường tròn đường kính AD. 2 đường chéo AC và DB cắt nhau tại E, EF vuông góc AD. đường thẳng CF cắt đường tròn tại điểm thứ 2 là M. BD giao CF tại N.cm
a, tg CEFD nội tiếp
b, tian Fa là phân giác của góc BFM
c, BE.DN=EN.BD
d,K là trung điểm DE
cm tg CBKF nội tiếp được

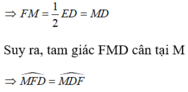
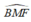 là góc ngoài tại đỉnh M của tam giác FMD nên:
là góc ngoài tại đỉnh M của tam giác FMD nên:
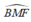 và
và  và cùng nhìn cạnh BF dưới một góc bằng nhau
và cùng nhìn cạnh BF dưới một góc bằng nhau

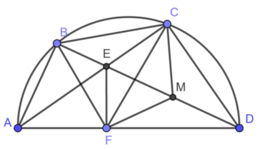

Bạn tự vẽ hình nha
a) ACD chắn nửa đường tròng => ACD = 90 => ECD = 90 độ
TG CEFD có ECD + EFD = 90 + 90 = 180 => CEFD nội tiếp
b), Vì tg CEFD nội tiếp => EFC = CDE ( cùng chắn cung CE ) (1)
ABCD nội tiếp => CDB = BAC ( cùng chắn cug BC ) (2)
CMTT BAFE là tứ giác nội tiếp => BFE = BAE ( cùng chắn cung BE ) hay BAC = BFE (3)
Từ (1) (2) và (3) => BFE = CFE
=> BFA = CFD ( cùng phụ hai góc bằng nhau ) mà CFD = AFM => BFA = AFM
=> FA là tia p/g BFM
c) VÌ BFE = EFN => EF là tia pg BFN => \(\frac{BF}{FN}=\frac{BE}{EN}\) ( tc đường p/g trong tam giác )
VÌ FA là tia pg BFM => FA là tia p/g góc ngoài của BFN ( Vì BFM ; BFN là hai góc kề bù )
=> \(\frac{BF}{FN}=\frac{DB}{DN}\left(II\right)\)
Từ (I) và ( II ) => \(\frac{BE}{EN}=\frac{BD}{DN}\Rightarrow BE\cdot DN=BD\cdot EN\)
d) TAm giác EFD vuông tại F có FK là trung tuyến => FK = KD => KFD cân tại K => KFD = KDF
MÀ KDF = BCA ( góc nội tiếp cùng chắn cung AB ) => KFD = BCA
TAm giác ECD vuông tại C có CK là tiếp tuyến => CK = KD => KCD = KDC mà CDK = BAC (CMT )
=> KCD = BAC mà EFB = BAC ( CMT ) => KCD = BFE => BFA = ECK ( cùng phụ hai góc bằng nhau )
TG BCKF có BCK + BFK = BCA + ECK + BFK = BFA + BFK + KFD = AFD = 180 độ
=> BCKF là tứ giác nội tiếp
Xem lại giúp mình nha ...............
bài này để mk về nghĩ nhé mai mk trả lời cho