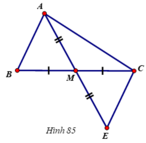
cho tam giác ABC, M là trung điểm của BC.trên tia đối của tia MA lấy điểm E sao cho ME=MA. Chứng minh rằng AB//CE
a.) Vẽ hình theo yêu cầu.
b.) Ghi giả thiết,kết luận.
c.) Chứng minh hai tam giác bằng nhau.
d.) Từ đó suy ra hai góc so le trong (hoặc đồng vị) bằng nhau thì AB//CE.)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

- Thứ tự sắp xếp là 5, 1, 2, 4, 3
Tam giác AMB và tam giác EMC có
MB = MC (gt)
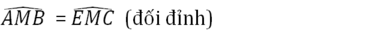
MA = ME (gt)
Do đó ΔAMB = ΔEMC (c.g.c)


Xét tam giác ABM và tam giác MCE có
- BM = MC (Vì M là trung điểm BC)
-ME = MA ( giả thiết )
- góc BMA = góc CME (đối đỉnh)
Vậy tam giác ABM = tam giác MCE
=> góc BAM = góc CEM
=> AB//CE
Xét Δ ABM và Δ ECM có:
ME=MA ( theo giả thiết )
góc BMA= góc CME (đối đỉnh )
BM=CM ( do M là trung điểm của BC )
→ Δ ABM=Δ ECM ( C-G-C)
→ góc BAM= góc CEM
Mà 2 góc này ở vị trí so le trong nên AB //CE.

a, Xét △ABC và △DCE có
AC = CD
C^ đối đỉnh
BC = CE
=> △ABC = △DCE
b, VÌ △ABC = △DCE nên góc BAC = góc CDE
=> CDE = 90 độ
c, Vì BE = BC + CE = 20
Mà BC = CE = \(\dfrac{BC}{2}\) = \(\dfrac{20}{2}\) = 10
Vì AD = AC + CD = 16
Mà AC = CD = \(\dfrac{AD}{2}\) = \(\dfrac{16}{2}\) = 8
Áp dụng định lý Pytago
ta có : \(BC^2=AB^2+AC^2\)
\(10^2=AB^2+8^2\)
\(100=AB^2+64\)
\(AB^2=100-64=36\)
Vậy \(AB=6^2\)
Mong bạn tick cho mik :))

Bạn tự vẽ hình nhé !
Xét \(\Delta AMB\)và \(\Delta ECM\)có:
\(MA=ME\left(gt\right)\)
\(MB=MC\)( vì M là trung điểm BC )
\(\widehat{BMA}=\widehat{EMC}\)( 2 góc đối đỉnh )
\(\Rightarrow\Delta AMB=\Delta ECM\left(c.g.c\right)\)
Vì \(\Delta AMB=\Delta ECM\left(cmt\right)\)
\(\Rightarrow\widehat{BAM}=\widehat{MEC}\)( 2 góc tưởng ứng )
Mà 2 góc này ở vị trí so le trong
\(\Rightarrow AB//CE\)
\(\text{a) xét tam giác AMB và tam giác EMC}\)
\(\text{có : MB=MC( M là trung điểm của BC)}\)
\(\text{góc AMB=góc EMC( đ đ)}\)
\(\text{AM=EM(gt)}\)
=> tam giác AMB=tam giác EMC(c-g-c)
\(\text{b) xét tam giác AMB và tam giác CME}\)
\(\text{có: AM=EM(gt)}\)
\(\text{góc AMB=góc CME (đ đ)}\)
\(\text{MB=MC(M là trung điểm của BC)}\)
=> tam giác AMB=tam giác CME(c-g-c)
=> góc CAM= góc MEC ( 2 góc tương ứng)
\(\text{mà 2 góc này ở vị trí so le trong}\)
=> AC=CE ( 2 cạnh tương ứng)

a/ Trong TG ABC : AB2=BC2-AC2 (đ/l Pytago đảo)
AB2=102-82=62
=> TG ABC là TG vuông .
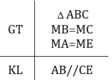
 5) Tam giác AMB và tam giác EMC có
5) Tam giác AMB và tam giác EMC có