Một đám vi khuẩn tại ngày thứ x có số lượng là N(x) Biết rằng N ' x = 2000 1 x và lúc đầu số lượng vi khuẩn là 5000 con. Vậy ngày thứ 12 số lượng vi...

PT

Pham Trong Bach

4 tháng 7 2018

Một đám vi khuẩn tại ngày thứ x có số lượng là N(x) Biết rằng N ' x = 2000 1 + x và lúc đầu số lượng vi khuẩn là 5000 con. Vậy ngày thứ 12 số lượng vi khuẩn (sau khi làm tròn) là bao nhiêu con? A. 10130. B. 5130. C. 5154. ...

Đọc tiếp

#Mẫu giáo

1

CM

Cao Minh Tâm

4 tháng 7 2018

Đáp án là A

Đúng(0)

PT

Pham Trong Bach

15 tháng 11 2017

Một đám vi khuẩn tại ngày thứ x có số lượng là N(x). Biết rằng N'(x) = 2000 1 + x và lúc đầu số lượng vi khuẩn là 5000 con. Vậy ngày thứ 12 số lượng vi khuẩn (sau khi làm tròn) là bao nhiêu con? A. 10130. B. 5130. C. 5154....

Đọc tiếp

#Toán lớp 12

1

CM

Cao Minh Tâm

15 tháng 11 2017

Chọn A.

Ta có ∫ 0 12 2000 1 + x d x = 2000 ln | 1 + x | 12 0 = 2000 ln 13 = N ( 12 ) - N ( 0 )

=> N(12) = 2000 ln13+ 5000 ≈ 10130

Đúng(0)

PT

Pham Trong Bach

8 tháng 10 2018

Một đám vi khuẩn tại ngày thứ t có số lượng là N(t). Biết rằng N ' ( t ) = 4000 1 + 0 , 5 t và lúc đầu đám vi khuẩn có 250000 con. Sau 10 ngày số lượng vi khuẩn xấp xỉ bằng: A. 264334 B. 263334 C.264254 ...

Đọc tiếp

#Toán lớp 12

1

CM

Cao Minh Tâm

8 tháng 10 2018

Số lượng vi khuẩn tại ngày thứ t bằng

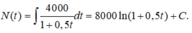
Bài tập trắc nghiệm Giải tích 12 | Câu hỏi trắc nghiệm Giải tích 12

Với t = 0 ta có: N(0) = 250000,

Vậy N(t) = 8000.ln(1 + 0,5t) + 250000

khi đó N(10) ≈ 264334.

Chọn A

Đúng(0)

PT

Pham Trong Bach

23 tháng 2 2017

Một đám vi trùng tại ngày thứ t có số lượng là N(t). Biết rằng N ' t = 2000 1 + 2 t và lúc đầu đám vi trùng có 300000 con. Ký hiệu L là số lượng vi trùng sau 10 ngày. Tìm L

A. L = 306089

B. L = 303044

C. L = 301522

D. L = 300761

#Mẫu giáo

1

CM

Cao Minh Tâm

23 tháng 2 2017

Chọn B.

Phương pháp : Sử dụng tích phân.

Cách giải : Ta có :

Đúng(0)

PT

Pham Trong Bach

3 tháng 1 2017

Một đám vi trùng tại ngày thứ t có số lượng là N(t). Biết rằng N ' t = 2000 1 + 2 t và lúc đầu đám vi trùng có 300000 con. Ký hiệu L là số lượng vi trùng sau 10 ngày. Tìm L A. 306089 B. 303044 C. 301522D. 300761 D....

Đọc tiếp

#Toán lớp 12

1

CM

Cao Minh Tâm

3 tháng 1 2017

Đúng(0)

PT

Pham Trong Bach

15 tháng 7 2019

Một đám vi trùng ngày thứ t có số lượng là N(t). Biết rằng N'(t)= 4000 1 + 0 , 5 t và lúc đầu đám vi trùng có 250000 con. Tính số lượng vi trùng sau 10 ngày (làm tròn đến hàng đơn vị) A. 264334 con B. 257167 con C. 258959 con D. 253584...

Đọc tiếp

#Mẫu giáo

1

CM

Cao Minh Tâm

15 tháng 7 2019

Đúng(0)

PT

Pham Trong Bach

10 tháng 7 2019

Sự tăng trưởng của một loài vi khuẩn được tính theo công thức f x = A e r x , trong đó A là số lượng vi khuẩn ban đầu, r là tỷ lệ tăng trưởng r > 0 , x (tính theo giờ) là thời gian tăng trưởng. Biết số vi khuẩn ban đầu có 1000 con và sau 10 giờ là 5000 con. Hỏi sau bao lâu thì số lượng vi khuẩn tăng gấp 10 lần A. 10 log 5 ...

Đọc tiếp

#Mẫu giáo

1

CM

Cao Minh Tâm

10 tháng 7 2019

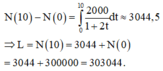
Đáp án C

Ta có 5000 = 1000 e 10 r ⇒ r = ln 5 10

Gọi x0 giờ là thời gian cần để vi khuẩn tang 10 lần,suy ra 10 A = A e ln 5 10 x 0 ⇒ x 0 = 10 log 5 10 giờ

Đúng(0)

HV

Hà Văn Minh Hiếu

18 tháng 2 2020 - olm

Một loại vi khuẩn cứ 30 phút thì tăng số lượng lên một số lần. Ban đầu, chỉ có 50 con vi khuẩn. Biết rằng sau 2 giờ thì số vi khuẩn đã là 4050 con. Hỏi sau 1 ngày, số vi khuẩn là bao nhiêu con?

#Toán lớp 8

1