Cho tam giác ABC cân tại đỉnh A. Biết độ dài cạnh đáy BC, đường cao AH và cạnh bên AB theo thứ tự lập thành cấp số nhân công bội q. Gía trị của q 2 bằng A. 2 ...

PT

Pham Trong Bach

29 tháng 9 2017

Cho tam giác ABC cân tại đỉnh A. Biết độ dài cạnh đáy BC, đường cao AH và cạnh bên AB theo thứ tự lập thành cấp số nhân công bội q. Gía trị của q 2 bằng A. 2 + 2 2 B. 2 − 2 2 C. 2 + 1 2 D. 2 − 1 2 ...

Đọc tiếp

#Mẫu giáo

1

CM

Cao Minh Tâm

29 tháng 9 2017

Đáp án là C

Đúng(0)

PT

Pham Trong Bach

30 tháng 11 2018

Cho tam giác ABC cân tại A, có đáy BC, đường cao AH, cạnh bên AB theo thứ tự đó lập thành một cấp số nhân. Hãy tính công bội q của cấp số nhân đó.

A. 2 2 + 1

B. 1 2 2 + 1

C. 1 2 2 2 + 1

D. 2 + 1

#Toán lớp 11

1

CM

Cao Minh Tâm

30 tháng 11 2018

Theo giả thiết AB=AC, BC,AH,AB lập thành cấp số nhân nên ta có hệ:

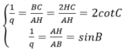
Từ đó ta có kết quả sau: 2cotC = sinC ⇔ 2cosC =sin2C = 1-cos2C

⇔ cos2C + 2cosC -1 =0 ⇒cosC = -1 +√2 (0° < C < 90°)

Do C là góc nhọn nên :

Cho nên công bội của cấp số nhân là:

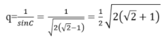
Đáp án C.

Đúng(0)

PT

Pham Trong Bach

20 tháng 3 2017

Cho tam giác ABC cân AB=AC cạnh đáy BC, đường cao AH, cạnh bên AB theo thứ tự đó lập thành một cấp số nhân. Công bội q của cấp số nhân đó là: A. 1 2 2 + 1 B. 1 2 2 . ( 2 + 1 ) C. 2 . ( 2 + 1 ) D. 2 ...

Đọc tiếp

#Mẫu giáo

1

CM

Cao Minh Tâm

20 tháng 3 2017

Đúng(0)

DH

Đỗ Hà Thọ

20 tháng 4 2016

Cho tam giác ABC cân (AB = AC), có cạnh đáy BC, đường cao AH, cạnh bên AB theo thứ tự đó lập thành một cấp số nhân. Hãy tính công bội q của cấp số nhân đó ?

#Toán lớp 11

1

TK

Trần Khánh Vân

20 tháng 4 2016

Theo giả thiết \(AB=AC,BC,AH,AB\) lập thành cấp số cộng cho nên ta có hệ :

\(\begin{cases}\frac{1}{q}=\frac{BC}{AH}=\frac{2HC}{AH}=2\cot C\\\frac{1}{q}=\frac{AH}{AB}=\sin B\end{cases}\)

Từ đó ta có kết quả :

\(2\cot C=\sin C\) hay \(2\cos C=\sin^2C=1-\cos^2C\)

\(\Leftrightarrow\cos^2C+2\cos C-1=0\)

\(\Leftrightarrow\cos C=-1+\sqrt{2}\) (0 < C < \(90^0\))

Do C là nhọn nên \(\sin C=\sqrt{2\left(\sqrt{2}-1\right)}\)

Cho nên công bội của cấp số nhân là : \(q=\frac{1}{\sin C}=\frac{1}{\sqrt{2\left(\sqrt{2}-1\right)}}=\frac{1}{2}\sqrt{2\left(\sqrt{2}-1\right)}\)

Đúng(0)

PT

Pham Trong Bach

12 tháng 4 2019

Cho tam giác ABC cân tại A. Biết rằng độ dài cạnh BC, trung tuyến AM và độ dài cạnh AB theo thứ tự đó lập thành một cấp số nhân có công bội q. Tìm công bội q của cấp số nhân đó. ...

Đọc tiếp

#Toán lớp 12

1

CM

Cao Minh Tâm

12 tháng 4 2019

Đúng(0)

PT

Pham Trong Bach

14 tháng 9 2018

Cho tam giác ABC cân tại A. Biết rằng độ dài cạnh BC, trung tuyến AM và độ dài cạnh AB theo thứ tự đó lập thành một cấp số nhân có công bội q. Tìm công bội q của cấp số nhân đó A. q = 1 + 2 2 B. q = 2 + 2 2 2 C. q = − 1 + 2 2 D. q = − 2 + 2 2 2 ...

Đọc tiếp

#Mẫu giáo

1

CM

Cao Minh Tâm

14 tháng 9 2018

Đáp án B

Ta có

A M 2 + B C 2 2 = A B 2 B C . A B = A M 2 ⇒ B C . A B + B C 2 2 = A B 2 ⇔ A B B C 2 − A B B C − 1 4 = 0

⇔ q 2 = A B B C = 1 + 2 2 ⇔ q = 1 + 2 2

Đúng(0)

PT

Pham Trong Bach

5 tháng 7 2018

Cho tam giác ABC cân tại A. biết rằng độ dài cạnh BC, trung tuyến AM và độ dài cạnh AB theo thứ tự đó lập thành một cấp số nhân có công bội q. tính công bội q của cấp số nhân đó A. q = 1 + 2 2 B. q = 2 + 2 2 2 C. q = - 1 + 2 2 D. q = - 2 + 2 2 2 ...

Đọc tiếp

#Mẫu giáo

1

CM

Cao Minh Tâm

5 tháng 7 2018

Đáp án B

Đúng(0)

PT

Pham Trong Bach

19 tháng 11 2018

Cho tam giác ABC cân tại A. Biết rằng độ dài cạnh BC, trung tuyến AM và độ dài cạnh AB theo thứ tự đó lập thành một cấp số nhân có công bội q. Tìm công bội q của cấp số nhân đó A. q = 1 + 2 2 B. q = 2 + 2 2 2 C. q = - 1 + 2 2 D. q = - 2 + ...

Đọc tiếp

#Toán lớp 11

1

CM

Cao Minh Tâm

19 tháng 11 2018

Chọn đáp án B

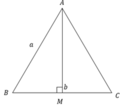
A B = a , B C = b ⇒ A M = a 2 - b 2 4

độ dài cạnh BC, trung tuyến AM và độ dài cạnh AB theo thứ tự đó lập thành một cấp số nhân

Đúng(0)

PT

Pham Trong Bach

5 tháng 1 2019

Cho tam giác ABC cân tại A. Biết rằng độ dài cạnh BC, trung tuyến AM và độ dài cạnh AB theo thứ tự đó lập thành một cấp số nhân có công bội q. Tìm công bội q của cấp số nhân đó. A. q = 1 + 2 2 B. q = 2 + 2 2 2 C. q = − 1 + 2 2 D. q = − 2 + 2 2 2 ...

Đọc tiếp

#Mẫu giáo

1

CM

Cao Minh Tâm

5 tháng 1 2019

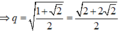
Đáp án B

Đặt B C = 2 x ⇒ A M = 2 q x , A B = 2 q 2 x .

Ta có: A B 2 = A M 2 + B M 2 ⇔ 2 q 2 x 2 = 2 q x 2 + x 2 ⇔ 4 q 4 − 4 q 2 − 1 = 0 ⇒ q 2 = 2 + 2 2 4

⇒ q = 2 + 2 2 2 .

Đúng(0)

PT

Pham Trong Bach

28 tháng 5 2018

Cho tam giác ABC cân tại A. Biết rằng độ dài cạnh BC, trung tuyến AM và cạnh AB theo thứ tự đó lập thành một cấp số nhân với công bội q. Tìm công bội q của cấp số nhân đó. A. q = 1 + 2 2 B. q = 2 + 2 2 2 C. q = - 1 + 2 2 D. q = - 2 + 2 2 2 ...

Đọc tiếp

#Mẫu giáo

1

CM

Cao Minh Tâm

28 tháng 5 2018

Đúng(0)

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP