Cho hàm số y = x + 1 2 x + 1 có đồ thị C . Tìm tất cả các giá trị thực của tham số m để đường thẳng d : y = m x + m + 1 2 cắt đồ thị C tại hai nghiệm phân biệt A, B sao cho O A 2 + O B 2 đạt giá trị nhỏ nhất (O là gốc tọa độ).
A. m = 1
B. m > 0
C. m ± 1
D. m = 2

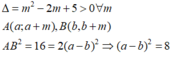
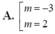

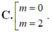
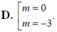
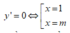
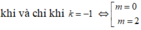
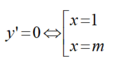
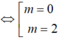

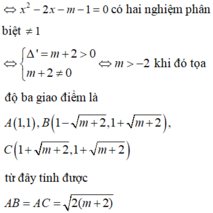
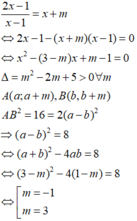
Đáp án A
Xét phương trình hoành độ giao điểm:
x + 1 2 x + 1 = m x + m + 1 2 ⇔ 4 m x 2 + 4 m x + m − 1 = 0 1
Phương trình (1) có 2 nghiệm x A ; x B ⇔ Δ ' = 4 m 2 − 4 m m − 1 = 4 m > 0 ⇔ m > 0.
Khi đó giao điểm của 2 đồ thị là A x A ; m x A + m + 1 2 ; B x B ; m x B + m + 1 2
với x A + x B = − 1 ; x A . x B = m − 1 4 m
Ta có O A 2 + O B 2 = x A 2 + m x A + m + 1 2 2 + x B 2 + m x B + m + 1 2 2 = m 2 + 2 m + 1 2 m = 1 + 1 2 m + 1 m ≥ 1 + 1 2 .2 = 2
( vì m > 0 , theo Cauchy ta có m + 1 m ≥ 2 . Dấu bằng xảy ra khi m = 1