Cho a , b , c ∈ R sao cho hàm số y = x 3 + a x 2 + b x + c đạt cực trị tại x = 3, đồng thời có y 0 = 3 và y 3 = 3 . Hỏi trong không gian Oxyz, điểm M a ; b ; c nằm trong mặt cầu nào sau đây?
A. x − 2 2 + y − 3 2 + z + 5 2 = 130.
B. x − 1 2 + y − 1 2 + z − 1 2 = 40.
C. x 2 + y 2 + z + 5 2 = 90.
D. x + 5 2 + y − 7 2 + z + 3 2 = 42.


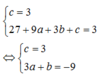
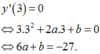


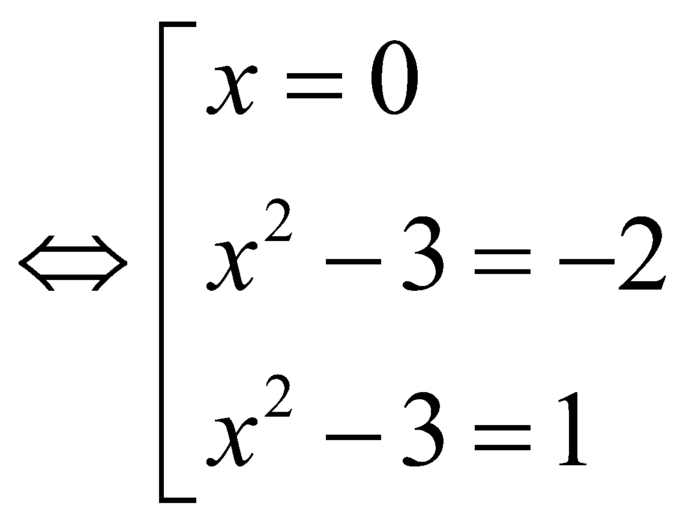
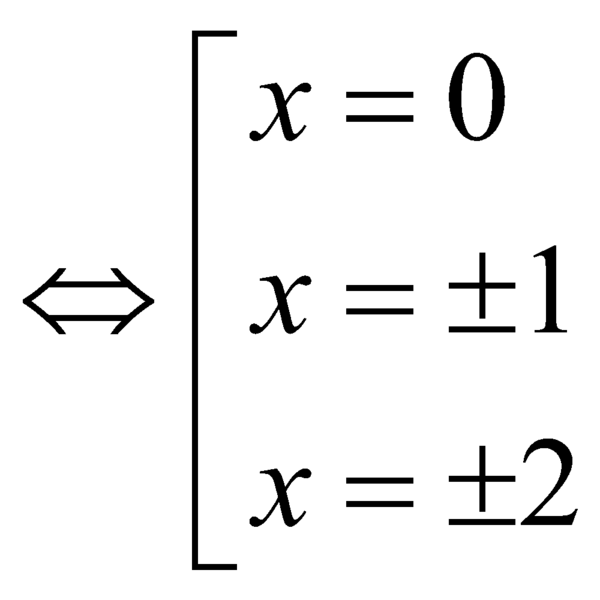 .
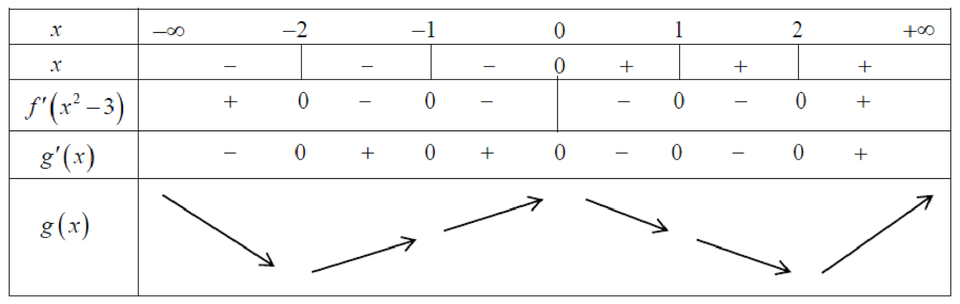
.
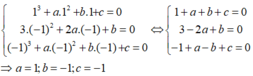
Đáp án D.
Từ y 0 = 3 và y 3 = 3 , ta có:
c = 3 27 + 9 a + 3 b + c = 3 ⇔ c = 3 3 a + b = − 9
Hàm số đạt cực trị tại x = 3 nên
y ' 3 = 0 ⇔ 3.3 2 + 2 a .3 + b = 0 ⇔ 6 a + b = − 27.
Do đó a = − 6 ; b = 9 ; c = 3. Do đó: M − 6 ; 9 ; 3 nằm trong mặt cầu ở đáp án D.
Chú ý: Điểm M nằm trong mặt cầu tâm I bán kính R khi và chỉ khi I M ≤ R .