Cho hàm số
f
x
có đạo hàm và liên tục trên đoạn
4
;
8
và
f
x
≠
0
∀
x
∈
4
;
8
.
Biết rằng
∫
4
8
f
'
x
2
f
x
4
d
x
=
1
và
f
4
=
1
4
,
f
8
=
1
2
. Tính
f
6
.
A.
5
8
.
...
Đọc tiếp
Cho hàm số f x có đạo hàm và liên tục trên đoạn 4 ; 8 và f x ≠ 0 ∀ x ∈ 4 ; 8 . Biết rằng ∫ 4 8 f ' x 2 f x 4 d x = 1 và f 4 = 1 4 , f 8 = 1 2 . Tính f 6 .
A. 5 8 .
B. 2 3 .
C. 3 8 .
D. 1 3 .
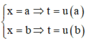
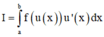
Đáp án D.
Ta có:
∫ 4 8 f ' x f x 2 d x = ∫ 4 8 f x − 2 d f x = f x − 1 − 1 4 8 = − 1 f 8 + 1 f 4 = − 2 + 4 = 2.
Gọi k là 1 hằng số thực. Xét
∫ 4 8 f ' x f 2 x + k 2 d x = ∫ 4 8 f ' x 2 f x 4 d x + 2 k ∫ 4 8 f ' x f 2 x d x + k 2 ∫ 4 8 d x = 1 + 2 k . k + 4 k 2 = 2 k + 1 2 .
Chọn k = − 1 2 , ta có ∫ 4 8 f ' x f 2 x − 1 2 2 d x = 0 , mà f ' x f 2 x − 1 2 2 ≥ 0 nên f ' x f 2 x − 1 2 2 = 0 ⇔ f ' x f 2 x = 1 2
⇒ ∫ f ' x f 2 x d x = x 2 + C ⇒ − 1 f x = x 2 + C .
Với x = 4 , ta có
− 1 f 4 = 2 + C ⇔ − 4 = 2 + C ⇔ C = − 6.
Do đó: f x = − 1 x 2 − 6 = 2 12 − x . Do đó f 6 = 2 12 − 6 = 2 6 = 1 3 .