Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng P : 2 x − 2 y + z − n = 0 và đường thẳng Δ : x − 1 2 = y + 1 1 = z − 3 2 m − 1 . Biết đường thẳng ∆ nằm trong mặt phẳng (P). Tổng m + n gần giá trị nào sau đây nhất?
A. 3.
B. 4.
C. 5.
D. 6.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Phương trình \(d_1\) : \(\dfrac{x-1}{1}=\dfrac{y-2}{-1}=\dfrac{z-3}{-1}\) dạng tham số: \(\left\{{}\begin{matrix}x=1+t\\t=2-t\\z=3-t\end{matrix}\right.\)
Gọi A là giao điểm d1 và (P), tọa độ A thỏa mãn:
\(3-t-1=0\Rightarrow t=2\Rightarrow A\left(3;0;1\right)\)
\(\overrightarrow{n_P}=\left(0;0;1\right)\) ; \(\overrightarrow{n_Q}=\left(1;1;1\right)\)
\(\overrightarrow{u_{\Delta}}=\left[\overrightarrow{n_P};\overrightarrow{n_Q}\right]=\left(-1;1;0\right)\)
\(\left[\overrightarrow{u_{\Delta}};\overrightarrow{n_P}\right]=\left(1;1;0\right)\)
Phương trình d: \(\left\{{}\begin{matrix}x=3+t\\y=t\\z=1\end{matrix}\right.\)

Chọn A
Vectơ pháp tuyến của mặt phẳng (P) là ![]() . Vectơ chỉ phương của đường thẳng d là
. Vectơ chỉ phương của đường thẳng d là ![]() . Phương trình tham số của đường thẳng
. Phương trình tham số của đường thẳng 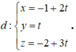
+ giao điểm của d và (P) :
Xét phương trình: -1 + 2t + 2t – 2 + 3t - 4 = 0 ó 7t – 7 = 0 ó t = 1. Suy ra giao điểm của đường thẳng d và mặt phẳng (P) là A (1;1;1)
Ta có: A ∈ Δ. Vectơ chỉ phương của đường thẳng Δ là:
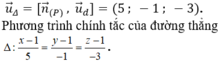
Đáp án là D