Cho hình chóp S.ABCD có S A ⊥ A B C D , ABCD là hình chữ nhật tâm O. Gọi I là trung điểm SC. Mệnh đề nào sau đây sai:
A. S D ⊥ D C
B. B D ⊥ S A C
C. B C ⊥ S B
D. O I ⊥ A B C D
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: OF là đường trung bình tam giác SAC
\(\Rightarrow OF//SA\Rightarrow OF//\left(SAD\right)\)
OE là đường trung bình tam giác SBD
\(\Rightarrow OE//SD\Rightarrow OE//\left(SAD\right)\)
\(\Rightarrow\left(OEF\right)//\left(SAD\right)\)

Đáp án A
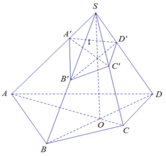
Xác định mặt phẳng (A’B’C’D’)
Lấy A’, B’, C’ lần lượt nằm trên SA, SB, SC
⇒ D’ thuộc mặt phẳng (A’B’C’)
Gọi O = AC ∩ BD
Trong (SAC) có: I = SO ∩ A ' C '
Trong (SBD) có: B ' I ∩ SD = D '
Từ cách dựng mặt phẳng (A’B’C’D’) ta thấy: SO, A’C’, B’D’ đồng quy tại I

Chọn C.
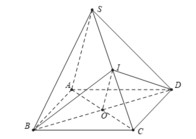
+) Ta có:
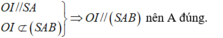
+) Ta có:
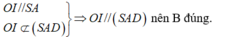
+) Ta có: mp (IBD) cắt hình chóp theo thiết diện là tam giác IBD nên C sai.
+) Ta có: (IBD) ∩ (SAC) = IO nên D đúng.

Đáp án C
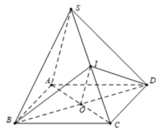
Ta có: O I / / S A O I ∉ S A B ⇒ O I / / S A B nên A đúng
Ta có: O I / / S A O I ∉ S A D ⇒ O I / / S A D nên B đúng
Ta có: (IBD)cắt hình chóp theo thiết diện là tam giác IBD nên
Ta có: I B D ∩ S A C = I O nên D đúng.
Đáp án B
C D ⊥ S A C D ⊥ A D ⇒ C D ⊥ S D
B C ⊥ A B B C ⊥ S A ⇒ B C ⊥ S A B
O I | | S A S A ⊥ A B C D ⇒ O I ⊥ A B C D
Do ABCD là hình chữ nhật nên không đảm bảo A C ⊥ B D , do đó không đảm bảo B D ⊥ S A C .