Vật chuyển động thẳng chậm dần đều với gia tốc có độ lớn 2m/s2 . Thời gian cần thiết để thay đổi vận tốc của vật từ 18m/s xuống còn 5m/s là bao nhiêu? Cách giải.
A.6.5s
B.6s
C.11,5s
D.10s
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
![]() , vật chuyển động chậm dần nên
, vật chuyển động chậm dần nên
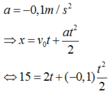
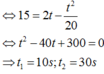
Mà từ phương trình vận tốc
![]()
Nghĩa là vật đổi chiều chuyển động tại t=20s. Nên tại t=30s vật đã đổi chiều chuyển động trước đó và quay về vị trí cách điểm xuất phát 15m. Do đó quãng đường vật đi được trong trường hợp này lớn hơn 15m. Vậy loại nghiệm t2=30s
Chú ý: Nếu lấy a thì phải thay ![]() ( tức là chọn chiều dương ngược chiều chuyển động ) và khi đó
( tức là chọn chiều dương ngược chiều chuyển động ) và khi đó
![]()

Chọn chiều dương là chiều chuyển động, gốc tọa độ trùng với vị trí ban đầu của vật, gốc thời gian là xuất phát.
a) Phương trình vận tốc: v = 6 + 4 t (m/s).
Đồ thị vận tốc - thời gian được biểu diễn như hình 12.
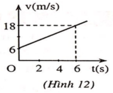
b) Khi v = 18 m/s thì t = 18 − 6 4 = 3 s.
Từ công thức v 2 − v 0 2 = 2 a s
quãng đường s = v 2 − v 0 2 2 a = 18 2 − 6 2 2.4 = 36 m.
c) Phương trình chuyển động: x = 6 t + 2 t 2 (m).
Khi v = 12 m/s thì t = 12 − 6 4 = 1 , 5 s ⇒ tọa độ x = 6.1 , 5 + 2.1 , 5 2 = 13 , 5 m.

Đáp án D
- Chọn gốc tọa độ tại vị trí lúc đầu của vật, gốc thời gian là lúc vật bắt đầu chuyển động
![]()
- Vật chuyển động theo chiều dương Ox nên v o >0 , suy ra v o = 20 m/s
Vật chuyển động chậm dần nên a v o <0 , vậy a = - 2m/ s 2
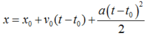
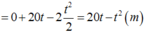

a) Phương trình chuyển động:
* Vật thứ nhất: x 1 = 5 t (m).
* Vật thứ hai: x 2 = 50 − t 2 (m).
b) Khi gặp nhau thì x 1 = x 2 ⇔ 5 t = 50 − t 2 hay t 2 + 5 t − 50 = 0 (*)
Giải phương trình (*) ta được: t 1 = 5 s; t 2 = − 10 s (loại).
Vị trí gặp nhau: x 1 = x 2 = 5.5 = 25 m.
Vậy hai vật gặp nhau tại thời điểm t = 5 s, tại vị trí cách A 25m.
c) Khi hai vật có vận tốc bằng nhau thì v 1 = v 2 = 5 m/s.
Phương trình vận tốc của vật thứ 2: v 2 = 2 t = 5 ⇒ t = 2 , 5 s .

Gia tốc của vật bằng
\(a=\dfrac{v^2-v_0^2}{2s}=\dfrac{15^2-0^2}{2\cdot60}=1,875\left(\dfrac{m}{s^2}\right)\)
Thời gian cần thiết đó là
\(t=\dfrac{v-v_0}{a}=\dfrac{5-18}{-2}=6,5\left(s\right)\)
mình cảm ơn ạ