Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi M, N là trung điểm của SA, SB. Mặt phẳng (MNCD) chia hình chóp đã cho thành hai phần. Tỉ số thể tích hai phần là (số bé chia số lớn)
A. 3 5
B. 3 4
C. 1 3
D. 4 5
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Đặt S M S A = x ( 0 < x < 1 )
Gọi thể tích của hình chóp S.ABCD là V.
V S . M N C V S . A B C = S M . S N . S C S A . S B . S C = x 2 ( 1 )
V S . M C D V S . A C D = S M . S D . S C S A . S C . S D = x ( 2 )
Ta có:
![]()
⇒ S A D C = 4 5 S A B C D
⇒ V S . A D C = 4 5 V S . A B C D = 4 5 V ; V S . A B C = V 5
Ta có:
V S . M N C = x 2 . V 5 ; V S . M C D = x 4 V 5
V 1 = V S . M N C + V S . M C D = V 5 ( x 2 + 4 x )
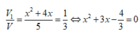
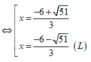
⇒ x = - 6 + 51 3

Chọn D.
Phương pháp:
+) Sử dụng công thức tỉ lệ thể tích:
Cho khối chóp S.ABC, các điểm A 1 , B 1 , C 1 lần lượt thuộc SA, SB, SC
+) Chia khối chóp đã cho thành các khối chóp nhỏ, tính thể tích của từng khối chóp.
Cách giải:
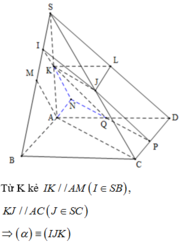
I,J lần lượt là trung điểm của SM, SC (do K là trung điểm của SA)
Trong (SAB), gọi N là giao điểm của IK và AB
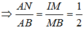
Trong (ABCD), kẻ đường thẳng qua N song song AC, cắt AD tại Q, CD tại P.
Khi đó, dễ dàng chứng minh P, Q lần lượt là trung điểm của CD, AD và

*) Gọi L là trung điểm của SD
Khi đó, khối đa diện SKJPQD được chia làm 2 khối: hình lăng trụ tam giác KJL.QPD và hình chóp tam giác S.KJL
