Cho hàm số y = f(x) liên tục trên các khoảng − ∞ ; 0 v à 0 ; + ∞ , có bảng biến thiên như sau
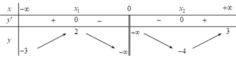
Tìm m để phương trình f x = m có 4 nghiệm phân biệt.
A. -3 < m < 2
B. -3 < m < 3
C. -4 < m < 2
D. -4 < m < 3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C
Từ đồ thị hàm số y=f’(x) ta có bảng biến thiên cho hàm số y=f(x) như sau:
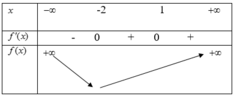
Nhìn vào bảng biến thiên ta thấy ngay trong khoảng (-2;+∞) thì hàm số y=f(x) đồng biến

![]()
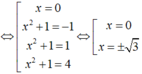
Các nghiệm trên đều là các nghiệm bội lẻ, do đó đều là cực trị của hàm số ![]()
Xét x = -1 ta có ![]()
từ đó ta có bảng xét dấu g’(x) như sau:
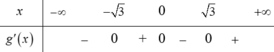
Dựa vào các đáp án ta thấy hàm số y = g(x) nghịch biến trên (0;1)
Chọn B

Chọn B.
Hàm số có nghĩa khi 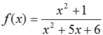 .
.
Vậy theo định lí ta có hàm số 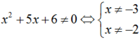 liên tục trên khoảng (-∞; -3); (-3; -2) và (-2; +∞).
liên tục trên khoảng (-∞; -3); (-3; -2) và (-2; +∞).

Chọn A.
Từ bẳng biến thiên suy ra hàm số đã cho đồng biến trên các khoảng (-∞;-1) và (0;1)
Chọn A
Dựa vào bảng biến thiên ta thấy phương trình có 4 nghiệm phân biệt khi -3 < m < 2.