Cho tam giác ABC vuông góc tại A, phân giác BD. So sánh các độ dài AB và AD
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
CM
11 tháng 1 2018
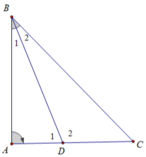
Cách 1. Xét tam giác ABD có ∠D2 là góc ngoài tam giác tại đỉnh D nên:
∠D2 = ∠B1 + ∠A
Suy ra: ∠D2 > ∠A (góc ngoài của ΔABD)
mà ∠A = 90o nên ∠D2 > 90o.
ΔBDC có ∠D2 > 90o nên ∠D2 > ∠C , do đó BC > BD.
Cách 2. Xét các đường xiên BD, BC.
Đoạn thẳng AD; AC lần lượt là hình chiếu của BD; BC trên đường thẳng AC.
Hình chiếu AC > AD nên đường xiên BC > BD. ( quan hệ đường xiên và hình chiếu của chúng ).
16 tháng 6 2023
a: ΔABD vuông tại A
=>BA<BD
b: Xét ΔCAE vuông tại A và ΔCAB vuông tại A có
CA chung
AE=AB
=>ΔCAE=ΔCAB
c: BA<BC
=>AD<CD
27 tháng 6 2023
a: Xét ΔBAD vuông tại A và ΔBHD vuông tại H có
BD chung
góc ABD=góc HBD
=>ΔBAD=ΔBHD
=>DA=DH
b: AD=DH
DH<DC
=>AD<DC
c: Xét ΔBKC có
KH,CA là đường cao
KH cắt CA tại D
=>D là trực tâm
=>BD vuông góc KC
12 tháng 4 2020
AD>AB
Áp dụng bài hình chiếu của tam giác vuông ấy bạn,hình như thế
16 tháng 12 2021
a: Xét ΔBAD và ΔBED có
BA=BE
\(\widehat{ABD}=\widehat{EBD}\)
BD chung
Do đó: ΔABD=ΔEBD
Suy ra: DA=DE
LL
16 tháng 12 2021
a) Vì BD là phân giác của ABC nên ABD = CBD
Xét Δ ABD và Δ EBD có:
BA = BE (gt)
ABD = EBD (cmt)
BD là cạnh chung
Do đó, Δ ABD = Δ EBD (c.g.c)
=> AD = DE (2 cạnh tương ứng) (đpcm)
b) Δ ABD = Δ EBD (câu a) => BAD = BED = 90o (2 góc tương ứng)
=> Δ DEC vuông tại E
Δ ABC vuông tại A có: ABC + C = 90o (1)
Δ CED vuông tại E có: EDC + C = 90o (2)
Từ (1) và (2) => ABC = EDC (đpcm)
c) Gọi giao điểm của AE và BD là H
Xét Δ ABH và Δ EBH có:
AB = BE (gt)
ABH = EBH (câu a)
BH là cạnh chung
Do đó, Δ ABH = Δ EBH (c.g.c)
=> BHA = BHE (2 góc tương ứng)
Mà BHA + BHE = 180o (kề bù) nên BHA = BHE = 90o
=> BH⊥AEBH⊥AE hay BD⊥AE(đpcm)
+) Xét tam giác BDC có ∠D1 là góc ngoài tam giác tại đỉnh D nên:
∠D1 = ∠B2 + ∠C
Suy ra: ∠D1 > ∠B2 (góc ngoài của ΔBDC)
Mà ∠B1 = ∠B2 ( vì BD là tia phân giác của góc ABC ) nên ∠D1 > ∠B1 .
ΔABD có ∠D1 > ∠B1 nên AB > AD.