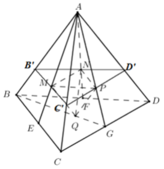
Cho khối tứ diện đều ABCD có thể tích V, M, N, P, Q lần lượt là trung điểm của AC, AD, BD, BC. Thể tích khối tứ diện AMNPQ là
A. V 6
B. V 3
C. V 4
D. 2 V 3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
19 tháng 6 2019
Ta có:
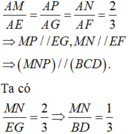
Ta có ∆ M N P đồng dạng với ∆ B C D theo tỉ số
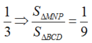
Dựng B ' C ' qua M và song song BC. C ' D ' qua P và song song với CD.
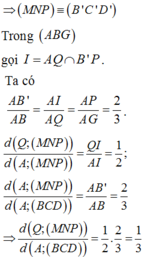
Chọn D.
CM
9 tháng 2 2019
Đáp án C
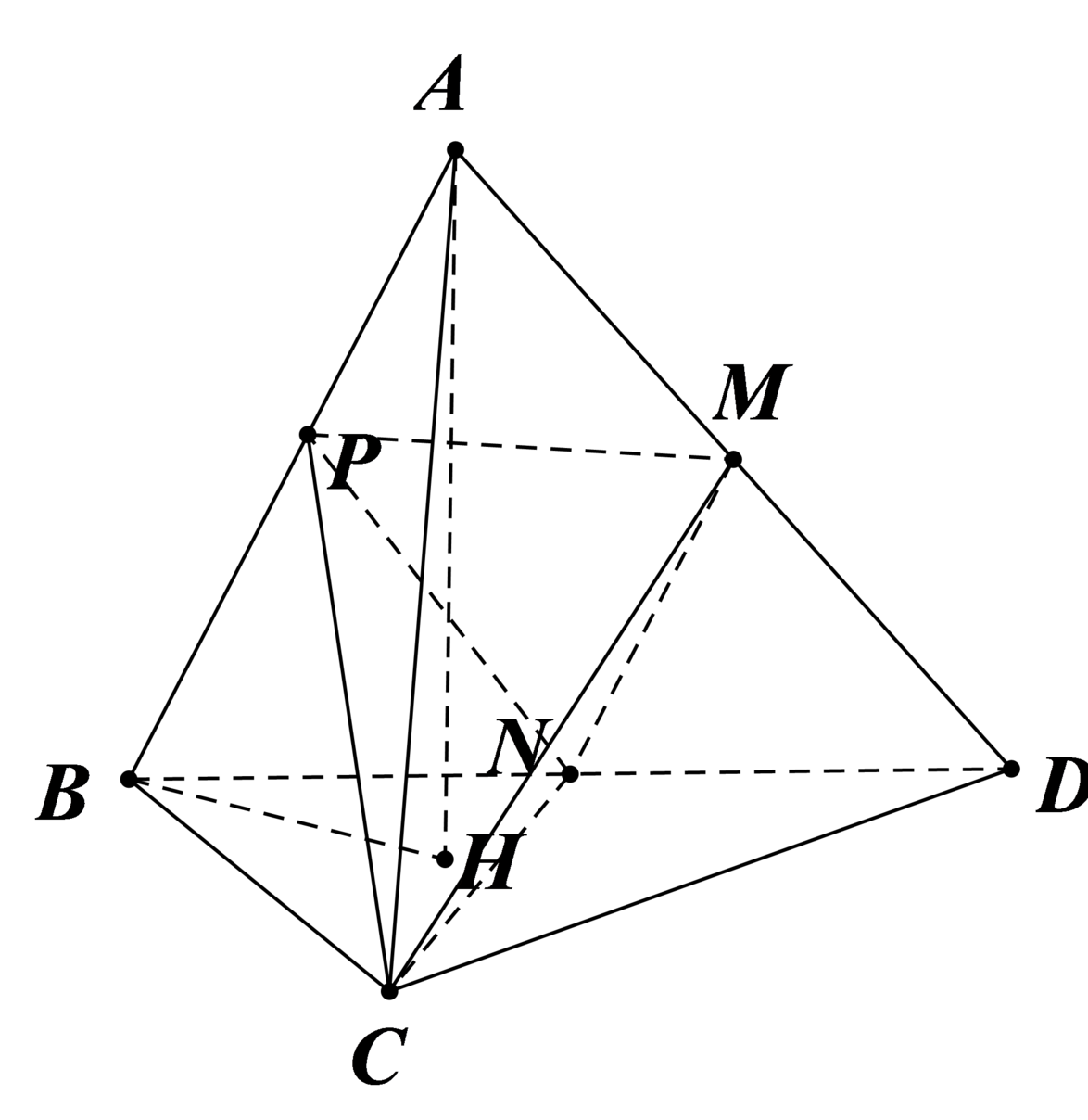
Gọi H là trọng tâm Δ B C D thì A H ⊥ B C D .
Ta có: B H = 2 3 . 3 3 2 = 3
⇒ A H = A B 2 − B H 2 = 9 − 3 = 6
Do đó: V A B C D = 1 3 . A H . S B C D = 1 3 . 6 . 3 2 3 4 = 9 2 4 .
Lại có:
V C . M N P V C . A B D = 1 3 d C , A B D . S M N P 1 3 d C , A B D . S A B D = S M N P S A B D = S A B D − S S P M − S D M N − S B P N S A B D = 1 − 1 2 . 2017 4035 − 1 4 − 1 2 . 2018 4035 = 1 4
Vậy V C . M N P = 1 4 . 9 2 4 = 9 2 16 .
CM
19 tháng 6 2018
Đáp án A
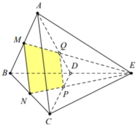
Nối 
chia khối tứ diện ABCD thành hai khối đa diện gồm PQD.NMB và khối đa diện chứa đỉnh A có thể tích A.
Dễ thấy P,Q lần lượt là trọng tâm của ∆BCE, ∆ABE
Gọi S là diện tích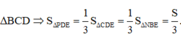 
Họi h là chiều cao của tứ diện ABCD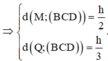 
Khi đó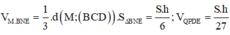 
Suy ra
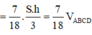
Đáp án C