cho tam giacs ABC có AB=AC=4cm.Gọi M là trung điểm của BC.Tính AM, biết BC=6cm
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Xét ΔABC có AH/AB=AK/AC
nên HK//BC
b: Xet ΔABC có HK//BC
nên AH/AB=HK/BC
=>HK/18=6/9=2/3
=>HK=12(cm)
c: Xét ΔABM có HI//BM
nên HI/BM=AI/AM
Xét ΔAMC có IK//MC
nên IK/MC=AI/AM
=>HI/BM=IK/MC
mà BM=CM
nên HI=IK
=>I là trung điểm của HK

Theo công thức đường trung tuyến:
\(AM^2=\dfrac{AB^2+AC^2}{2}-\dfrac{BC^2}{4}=\dfrac{9^2+11^2}{2}-\dfrac{10^2}{4}=76\Rightarrow AM=2\sqrt{19}\)
\(BN^2=\dfrac{AB^2+BM^2}{2}-\dfrac{AM^2}{4}=\dfrac{9^2+\dfrac{1}{4}.10^2}{2}-\dfrac{76}{4}=34\Rightarrow BN=\sqrt{17}\)

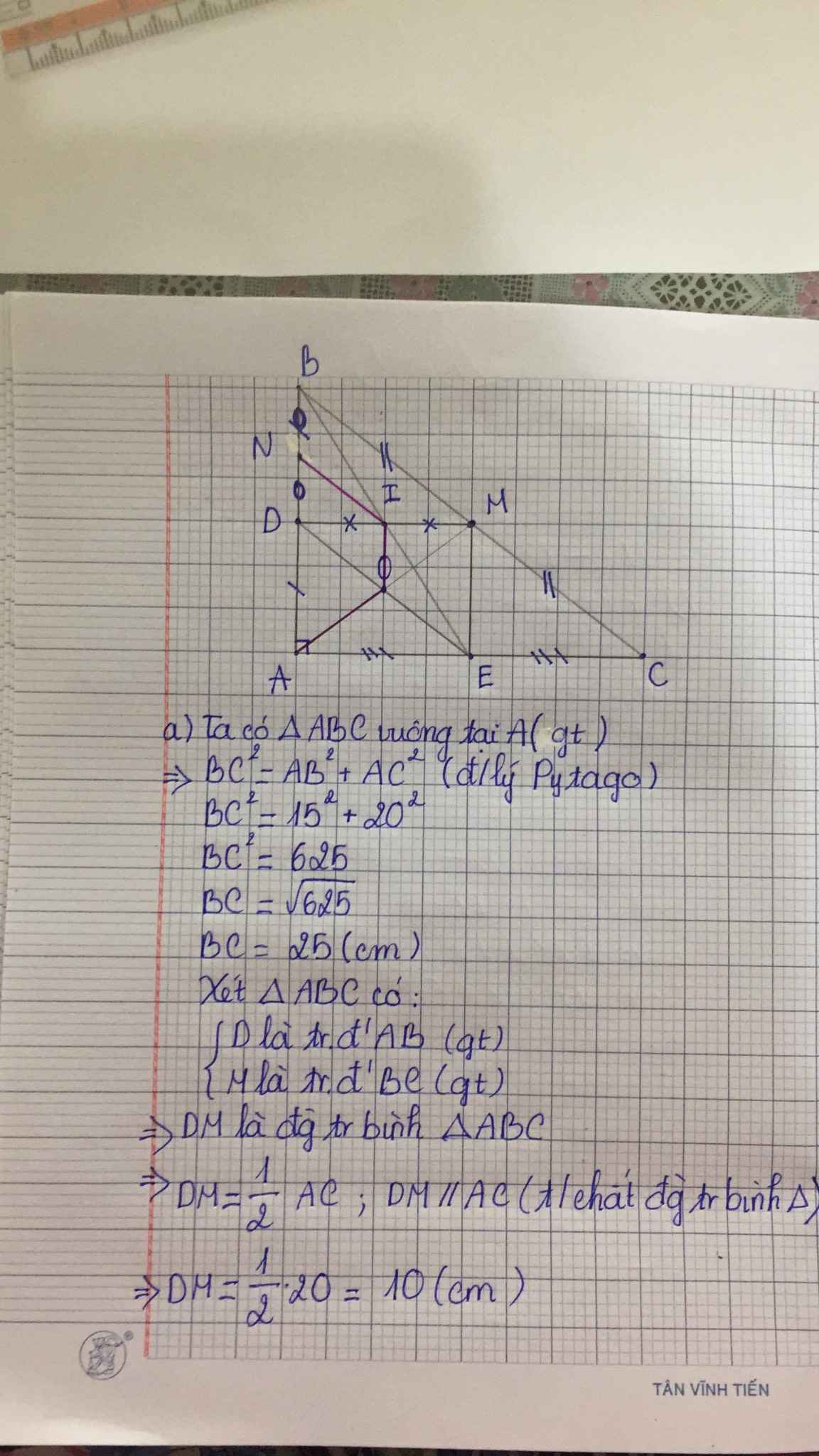
a: Xét ΔABC vuông tại A có \(BC^2=AB^2+AC^2\)
hay BC=25(cm)
Xét ΔABC có
D là trung điểm của AB
M là trung điểm của BC
Do đó: DM là đường trung bình của ΔABC
Suy ra: \(DM=\dfrac{AC}{2}=10\left(cm\right)\)

Goi G là diem doi xung voi A qua M.
Cm dc AG=4+4=8,CG=BA=6,AB=CG=6 (ACGB là hbh)
Suy ra tg ACG vuong tai G (Pythagoras dao,6^2+8^2=10^2)
Suy ra goc AGC=90°
Suy ra goc MAB=90° (AB//CG).
đã chứng minh xong
_______HẾT_________
Gọi L là điểm đối xứng với A qua M.
Dễ dàng cm ABGC là hình bình hành \(\Rightarrow\)AB=CG=6 cm
Lại có AG=8 cm, áp dụng định lý Pitago đảo vào tam giác ACG, ta suy ra tam giác AGC vuông tại G(\(8^2+6^2=10^2\)
Lại có tam giac BAG= tam giác CGA . Do đó góc MAB= 90 độ

Ta có :
a)
Diện tích hình tam giác ABC là :
24 x 16 : 2 = 192 ( cm2 )
b)
Chiều cao AN của hình tam giác ACN là :
16 : 2 = 8 ( cm )
Diện tích hình tam giác ACN là :
24 x 8 : 2 = 96 ( cm2 )
Độ dài đáy AM của hình tam giác AMN là :
24 : ( 1 + 3 ) x 1 = 6 ( cm )
Diện tích hình tam giác AMN là :
6 x 8 : 2 = 24 ( cm2 )
Đ/S : a ) 192 cm2
b ) 96 cm2
24 cm2
k nha !!!!!!

AB = AC suy ra tam giác ABC cân tại A
Biết BM = CM = 6 / 2 = 3 ( M là trung điểm của BC )
Tam giác ABM vuông tại A
AM = AB2 - BM2
AM = 42 - 32
AM = 5 ( đl Pytago )