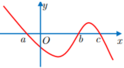
Cho hàm số y = f(x) xác định trên ℝ . Đồ thị hàm số y = f '(x) cắt trục hoành tại ba điểm có hoành độ a , b , c a < b < c như hình vẽ. Biết f (b)<0, hỏi phương trình f(x) = 0 có nhiều nhất bao nhiêu nghiệm?
A. 1.
B. 2.
C. 3.
D. 4.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Trên khoảng ( a ; b ) và ( c ; + ∞ ) hàm số đồng biến vì y'>0 đồ thị nằm hoàn toàn trên trục Ox
Hàm số nghịch biến trên các khoảng ( - ∞ ; a ) và (b;c) vì y'<0
Suy ra x=b là điểm cực đại mà y(b) <0 do đó trục hoành cắt đồ thị tại hai điểm phân biệt. Với d<0 ta có

+ Ta có y ' = f ' ( x ) = a d - b c ( c x + d ) 2 . Từ đồ thị hàm số y= f’(x) ta thấy:
Đồ thị hàm số y= f’(x) có tiệm cận đứng x=1 nên –d/c= 1 hay c= -d
Đồ thị hàm số y= f’(x ) đi qua điểm (2;2)
⇒ a d - b c ( 2 c + d ) 2 = 2 ↔ a d - b c = 2 ( 2 c + d ) 2
Đồ thị hàm số y= f’(x) đi qua điểm (0;2)
⇒ a d - b c d 2 = 2 ↔ a d - b c = 2 d 2
Đồ thị hàm số y=f(x) đi qua điểm (0;3) nên b/d= 3 hay b= 3d
Giải hệ gồm 4 pt này ta được a=c= -d và b= 3d .
Ta chọn a=c= 1 ; b= -3 ; d= -1
⇒ y = x - 3 x - 1
Chọn D.

Đáp án A
Dựa vào đồ thị của hàm số y = f '(x), em suy ra được bảng biến thiên như sau:
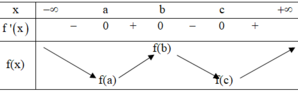
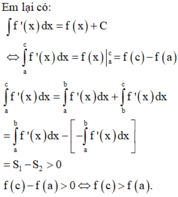

Chọn A
Đồ thị của hàm số ![]() liên tục trên các đoạn
liên tục trên các đoạn ![]() và
và ![]() , lại có
, lại có ![]() là một nguyên hàm của
là một nguyên hàm của ![]() .
.
Do đó diện tích của hình phẳng giới hạn bởi các đường:
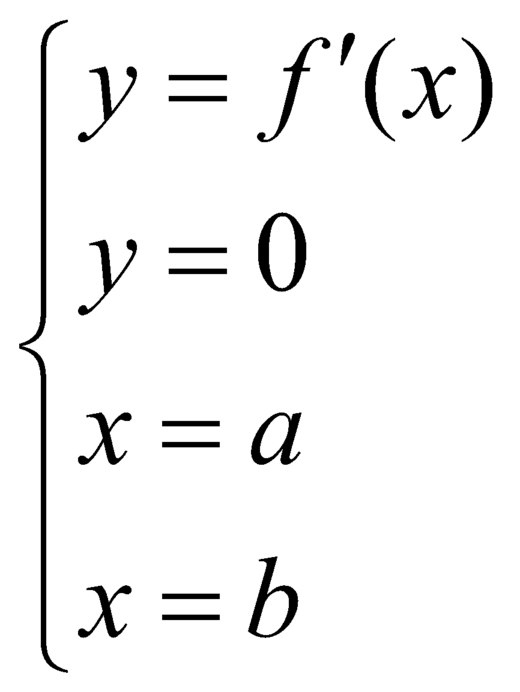 là:
là:
![]() .
.
Vì ![]()
![]()
Tương tự: diện tích của hình phẳng
giới hạn bởi các đường: 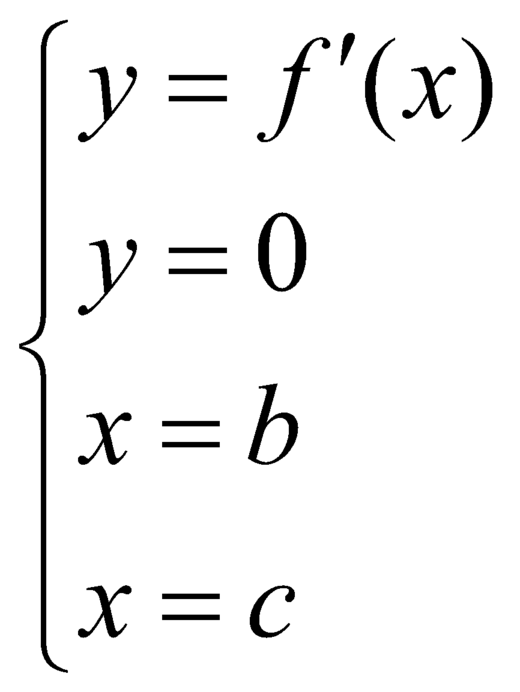 là:
là:
![]() .
.
![]()
![]() .
.
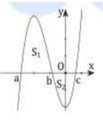
Mặt khác, dựa vào hình vẽ ta có: ![]()
![]() .
.
Từ (1), (2) và (3) ta chọn đáp án A.
( có thể so sánh ![]() với
với ![]() dựa vào dấu của
dựa vào dấu của ![]() trên đoạn
trên đoạn ![]() và so sánh
và so sánh ![]() với
với ![]() dựa vào dấu của
dựa vào dấu của ![]() trên đoạn
trên đoạn ![]() )
)

Chọn D
Ta có
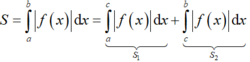
Vì f(x) < 0, ∀ x ∈ a ; c nên |f(x)| = –f(x).
Do đó, S 1 = - ∫ a c f x d x .
Tương tự, f(x) > 0, ∀ x ∈ a ; c nên |f(x)| = f(x).
Do đó, S 2 = ∫ c b f x d x .
Vậy S = - ∫ a c f x d x + ∫ c b f x d x .

Đáp án D
Ta có: y ' = 3 a x 2 + 2 b x + c
+) Đồ thị hàm số f'(x) đi qua gốc tọa độ => c=0
+) Đồ thị hàm số f'(x) có điểm cực trị:
1 ; − 1 ⇒ 6 a + 2 b = 0 3 a + 2 b = − 1 ⇔ a = 1 3 b = − 1
Vậy hàm số f ' x = x 2 − 2 x . Đồ thị hàm số f(x) tiếp xúc với trục hoành nên có cực trị nằm trên trục hoành. Các giá trị cực trị của hàm số f(x) là:
f 0 = d f 2 = 8 3 − 4 + d = − 4 3 + d
do điểm tiếp xúc có hoành độ dương
=> d = 4 3 => f(x) cắt trục tung tại điểm có tung độ 4 3

+Ta có đạo hàm f’ (x)= 3ax2+ 2bx+c .
+ Dựa vào đồ thị hàm số y= f’ ( x) ta thấy đồ thị hàm số đi qua các điểm (0 ; 0) ; (1 ; -1) ; (2 ; 0) nên a= 1/3 ; b= -1 ; c= 0.
Do vậy hàm số cần tìm có dạng y= 1/3 x3-x2+ d .
Điểm tiếp xúc với trục hoành là cực trị của đồ thị hàm số và tại đó ta có x= 0 hoặc x= 2. + Vì đồ thị hàm số y= f(x) tiếp xúc với trục hoành tại điểm có hoành độ dương nên đồ thị hàm số tiếp xúc trục hoành tại điểm x= 2 nghĩa là:
f( 2) = 0 hay 8/3-4+ d= 0 nên d= 4/3
Chọn D.
Đáp án là D
Từ đồ thị f ’(x) ta lập được BBT của f(x)
=> Có 4 nghiệm là nhiều nhất