Cho lăng trụ A B C . A ' B ' C ' . Gọi M, N lần lượt là trung điểm của AA' và BC' . Khi đó đường thẳng AB' song song với mặt phẳng:
A. (C'MN)
B. (A'CN)
C. (A'BN)
D. (BMN)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
20 tháng 3 2018
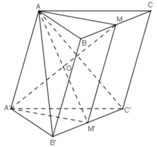
a) Do ABC.A’B’C’ là hình lăng trụ nên ta có: BCC’B’ là hình bình hành
Xét tứ giác BCC’B’ có M và M’ lần lượt là trung điểm của BC và B’C’ nên MM’ là đường trung bình
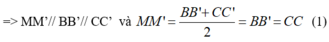
Lại có: AA’// BB’ và AA’= BB’ ( tính chất hình lăng trụ) (2)
Từ (1) và (2) suy ra: MM’// AA’ và MM’ = AA’
=> Tứ giác AMM’A’ là hình bình hành
b) Trong (AMM’A’) gọi O = A’M ∩ AM’, ta có :
Ta có : O ∈ AM’ ⊂ (AB’C’)
⇒ O = A’M ∩ (AB’C’).
c)
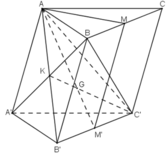
Gọi K = AB’ ∩ BA’, ta có :
K ∈ AB’ ⊂ (AB’C’)
K ∈ BA’ ⊂ (BA’C’)
⇒ K ∈ (AB’C’) ∩ (BA’C’)
Dễ dàng nhận thấy C’ ∈ (AB’C’) ∩ (BA’C’)
⇒ (AB’C’) ∩ (BA’C’) = KC’.
Vậy d cần tìm là đường thẳng KC’
d) Trong mp(AB’C’), gọi C’K ∩ AM’ = G.
Ta có: G ∈ AM’ ⊂ (AM’M)
G ∈ C’K.
⇒ G = (AM’M) ∩ C’K.
+ K = AB’ ∩ A’B là hai đường chéo của hình bình hành ABB’A’
⇒ K là trung điểm AB’.
ΔAB’C’ có G là giao điểm của 2 trung tuyến AM’ và C’K
⇒ G là trọng tâm ΔAB’C’.
Q
31 tháng 3 2017
a) Do MM' lần lượt là trung điểm của BC và B'C' nên M'M//BB'//CC'. Vì vậy MM'//AA'.
Vì vậy tứ giác A'M'MA là hình bình hành. Suy ra: AM//A'M'.
b) Trong mp (AA'M'M), ta có: MA' ∩ AM' = K.
Do \(K\in A'M\) và \(A'M\in\left(AB'C'\right)\) nên K (AB'C').
c) Có \(O=AB'\cap A'B\) nên \(O\in\left(AB'C'\right)\cap\left(BA'C'\right)\).
Suy ra: \(d\equiv CO'\).
d) Trong (AB'C'): C'O ∩ AM' = G vì vậy G ( AMM') . Mà O, M' lần lượt là trung điểm AB' và B'C' nên G là trọng tâm của tam giác AB'C'.
Phương pháp:
Sử dụng quan hệ song song trong không gian để chứng minh và chọn đáp án đúng.
Cách giải: