Xét các số thực dương x;y thỏa mãn 2 l o g 3 x + x ( x + y ) ≥ l o g 3 8 - y + 8 x . Biểu thức P = 3 x + 2 y + 6 x + 18 y đạt giá trị nhỏ nhất tại x=a;y=b. Tính S=3a+2b.
A. 19
B. 20
C. 18
D. 17
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Ta có:
Đặt \(A=x+y+\dfrac{1}{x}+\dfrac{1}{y}\)
\(\Leftrightarrow A=x+y+\dfrac{4}{4x}+\dfrac{4}{4y}\)
\(\Leftrightarrow A=x+y+\dfrac{1}{4x}+\dfrac{3}{4x}+\dfrac{1}{4y}+\dfrac{3}{4y}\)
\(\Leftrightarrow A=\left(x+\dfrac{1}{4x}\right)+\left(y+\dfrac{1}{4y}\right)+\left(\dfrac{3}{4x}+\dfrac{3}{4y}\right)\)
\(\Rightarrow A\ge2\sqrt{x.\dfrac{1}{4x}}+2\sqrt{y.\dfrac{1}{4y}}+\dfrac{3}{4}.\dfrac{4}{x+y}\)
\(\ge2.\sqrt{\dfrac{1}{4}}+2\sqrt{\dfrac{1}{4}}+\dfrac{3}{4}.\dfrac{4}{1}\)
\(=2.\dfrac{1}{2}+2.\dfrac{1}{2}+3=1+1+3=5\)
Vậy ta có đpcm. Dấu"=" xảy ra\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{1}{4x}\\y=\dfrac{1}{4y}\\x=y\\x+y=1\end{matrix}\right.\) \(\Leftrightarrow x=y=\dfrac{1}{2}\left(tm\right)\)

\(\Leftrightarrow\left(x+y\right)^3-3xy\left(x+y\right)+\left(x+y\right)^3+30xy=2000\)
\(\Leftrightarrow2\left[\left(x+y\right)^3-1000\right]-3xy\left(x+y-10\right)=0\)
\(\Leftrightarrow2\left(x+y-10\right)\left[\left(x+y\right)^2-10\left(x+y\right)+100\right]-3xy\left(x+y-10\right)=0\)
\(\Leftrightarrow\left(x+y-10\right)\left[2\left(x+y\right)^2-20\left(x+y\right)+200-3xy\right]=0\)
\(\Leftrightarrow x+y=10\)
Do:
\(2\left(x+y\right)^2-20\left(x+y\right)+200-3xy\)
\(=\left(x+y-10\right)^2+\left(x+y\right)^2-3xy+100\)
\(=\left(x+y-10\right)^2+\left(x+\dfrac{y}{2}\right)^2+\dfrac{3y^2}{4}+100>0\)
https://hoc24.vn/cau-hoi/tim-xyin-z-biet-a2x2-xy-7x-2y-y2-70bx2-2y2-3xy-3x-5y-140ps-huong-dan-em-lam-chi-tiet-dang-nay-nua-voi-a.330915967066
Giúp e dạng này với anh . Cho e spam xíu :(

Đặt \(A=x+y+z+\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}\)
\(\Leftrightarrow A=x+y+z+\dfrac{9}{9x}+\dfrac{9}{9y}+\dfrac{9}{9z}\)
\(\Leftrightarrow A=x+y+z+\dfrac{1}{9x}+\dfrac{8}{9x}+\dfrac{1}{9y}+\dfrac{8}{9y}+\dfrac{1}{9z}+\dfrac{8}{9z}\)
\(\Leftrightarrow A=\left(x+\dfrac{1}{9x}\right)+\left(y+\dfrac{1}{9y}\right)+\left(z+\dfrac{1}{9z}\right)+\left(\dfrac{8}{9x}+\dfrac{8}{9y}+\dfrac{8}{9z}\right)\)
\(\Leftrightarrow A=\left(x+\dfrac{1}{9x}\right)+\left(y+\dfrac{1}{9y}\right)+\left(z+\dfrac{1}{9z}\right)+\dfrac{8}{9}.\left(\dfrac{1^2}{x}+\dfrac{1^2}{y}+\dfrac{1^2}{z}\right)\)
\(\Rightarrow A\ge2\sqrt{x.\dfrac{1}{9x}}+2\sqrt{y.\dfrac{1}{9y}}+2\sqrt{z.\dfrac{1}{9z}}+\dfrac{8}{9}.\dfrac{\left(1+1+1\right)^2}{x+y+z}\)
\(\Rightarrow A\ge2\sqrt{\dfrac{1}{9}}+2\sqrt{\dfrac{1}{9}}+2\sqrt{\dfrac{1}{9}}+\dfrac{8}{9}.\dfrac{3^2}{1}\)
\(\Rightarrow A\ge2.\dfrac{1}{3}.3+8=2+8=10\)
Vậy ta có BĐT cần chứng minh.
Dấu\("="\) xảy ra\(\Leftrightarrow x=y=z=\dfrac{1}{3}\)

Theo bài ra ta có:
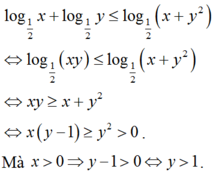
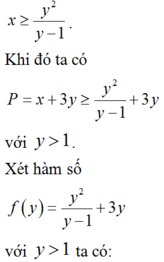
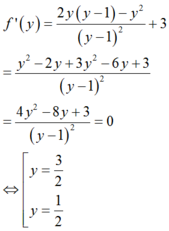
BBT:
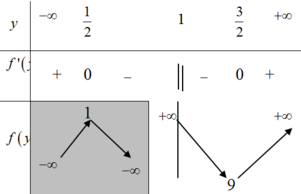
Từ BBT ta thấy
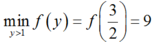
Vậy P ≥ 9 hay P m i n = 9 .
Chọn C.

\(P=\dfrac{1}{x}+\dfrac{4}{4y}\ge\dfrac{\left(1+2\right)^2}{x+4y}=\dfrac{9}{6}=\dfrac{3}{2}\)
Dấu "=" xảy ra khi \(\left(x;y\right)=\left(2;1\right)\)