Đồ thị (C) của hàm số y = x 3 - 3 x 2 + 4 và đường thẳng y = mx + m cắt nhau tại ba điểm phân biệt A(-1;0),B,C sao cho ∆ O B C có diện tích bằng 8 (O là gốc tọa độ). Mệnh đề nào đưới đây đúng ?
A. m là số nguyên tố.
B. m là số chẵn
C. m là số vô tỉ
D. m là số chia hết cho 3



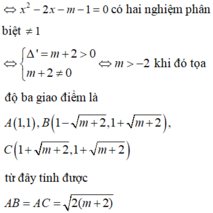



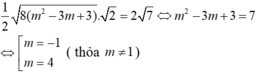

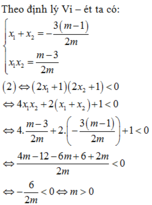
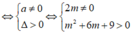
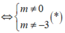
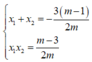
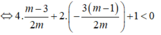
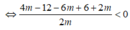
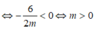
Đáp án B
x 3 - 3 x 2 + 4 = m x + m
⇔ x 3 - 3 x 2 - m x + 4 - m = 0
⇔ ( x + 1 ) ( x 2 - 4 x + 4 - m ) = 0
Gọi B ( x 1 ; m x 1 + m ) ; C ( x 2 ; m x 2 + m )
B C = ( x 2 - x 1 ) 2 + ( m x 2 - m x 1 ) 2 = m 2 + 1 . ( x 2 + x 1 ) 2 - 4 x 1 x 2 = m 2 + 1 . 16 - 4 ( 4 - m ) = 2 m 2 + 1 . m
Mà d ( O ; B C ) = d ( O ; d )
d là đường thẳng m x - y + m . Suy ra d(O;d)= m m 2 + 1
Ta có
S O B C = 1 2 . d ( O ; B C ) . B C
Theo giả thiết, ta được
m m = 8 ⇒ m = 4