Cho hàm số g ( x ) = x 2 + 1 và hàm số f ( x ) = x 3 - 3 x 2 + 1 . Tìm m để phương trình f ( g ( x ) ) - m = 0 có 4 nghiệm phân biệt.
A. - 3 < m < 1
B. - 3 < m ≤ 1
C. - 3 ≤ m ≤ - 1
D. m > - 1
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

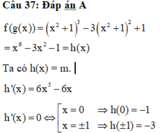
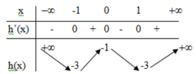

Đáp án B
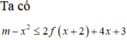
![]()
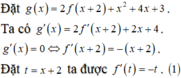
(1) là phương trình hoành độ giao điểm của đồ thị f'(t) và đường thẳng d : y = -t (hình vẽ)
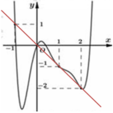
Dựa vào đồ thị của f'(t) và đường thẳng y =-t ta có




Chọn B.
Ta có: f(x + 1) = log2(x + 1) và g(x + 2) = log2(2 - x)
![]()
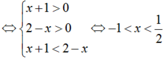

Đáp án C
Với f x > 0 , ∀ x ∈ ℝ . Xét biểu thức f ' x f x = 2 - 2 x *
Lấy nguyên hàm 2 vế (*), ta được ∫ d f x f x = ∫ 2 - 2 x d x
⇔ ∫ d f x f x = - x 2 + 2 x + C ⇔ ln f x = - x 2 + 2 x + C
Mà f(0) =1 suy ra C = lnf(0) = ln1 = 0. Do đó f x = e - x 2 + 2 x
Xét hàm số f x = e - x 2 + 2 x trên - ∞ ; + ∞ , có f ' x = - 2 x + 2 = 0 ⇔ x = 1
Tính giá trị f 1 = e ; lim x → - ∞ f x = 0 ; lim x → - ∞ f x = 0
Suy ra để phương trình f(x) = m có hai nghiệm thực phân biệt ⇔ 0 < m < e .

\(g'\left(x\right)=0\Rightarrow x=0\)
Ta thấy \(g\left(x\right)\) đồng biến trên \(\left(0;+\infty\right)\)
\(\Rightarrow g\left(f\left(x\right)\right)\) đồng biến khi \(f\left(x\right)\ge0\)
\(\Rightarrow g\left(f\left(x\right)\right)\) đồng biến trên \(\left(3;+\infty\right)\) khi \(f\left(x\right)\ge0\) ; \(\forall x>3\)
\(\Leftrightarrow x^2-4x\ge-m\) ; \(\forall x>3\)
\(\Leftrightarrow-m\le\min\limits_{x>3}\left(x^2-4x\right)\)
\(\Rightarrow-m\le-3\Rightarrow m\ge3\)