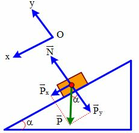
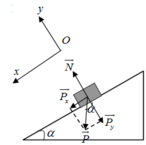
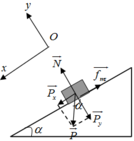
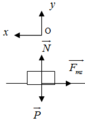
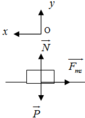
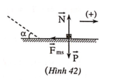
Một vật trượt từ mặt phẳng nghiêng cao 0,8m, dài 2m và g=10m/s2. Bỏ qua ma sát giữa vật và mặt phẳng nghiêng, khi xuống đến mặt phẳng ngang vật tiếp tục trượt trên mặt phẳng ngang với hệ số ma sát là μ=0,2.Tính:a)Gia tốc của vật trên mặt phẳng nghiêngb)Vận tốc của vật tại chân mặt phẳng nghiêngc)Thời gian vật chuyển động xuống mặt phẳng nghiêngd)Gia tốc của vật tại mặt phẳng ngange)Quãng...
Đọc tiếp
Một vật trượt từ mặt phẳng nghiêng cao 0,8m, dài 2m và g=10m/s2. Bỏ qua ma sát giữa vật và mặt phẳng nghiêng, khi xuống đến mặt phẳng ngang vật tiếp tục trượt trên mặt phẳng ngang với hệ số ma sát là μ=0,2.Tính:
a)Gia tốc của vật trên mặt phẳng nghiêng
b)Vận tốc của vật tại chân mặt phẳng nghiêng
c)Thời gian vật chuyển động xuống mặt phẳng nghiêng
d)Gia tốc của vật tại mặt phẳng ngang
e)Quãng đường tối đa vật đi được trên mặt phẳng ngang
f)Thời gian vật chuyển động trên mặt phẳng ngang.
(1)
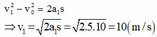
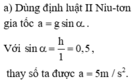
Đáp án:
a.a=2,167m/s2b.v=1,862m/sc.t=0,86sd.a′=−2m/s2e.s′=0,8668mf.t′=0,931sa.a=2,167m/s2b.v=1,862m/sc.t=0,86sd.a′=−2m/s2e.s′=0,8668mf.t′=0,931s
Giải thích các bước giải:
a.
Ta có:
sinα=0,82=0,4cosα=√1−sin2α=√1−0,42=√215sinα=0,82=0,4cosα=1−sin2α=1−0,42=215
Áp dụng định luật II Niu tơn:
⃗P+⃗Fms+⃗N=m⃗a+oy:N=Pcosα+ox:Psinα−Fms=ma⇒a=Psinα−Fmsm=mgsinα−μmgcosαm=gsinα−μgcosα=10.0,4−0,2.10.√214=2,167m/s2P→+F→ms+N→=ma→+oy:N=Pcosα+ox:Psinα−Fms=ma⇒a=Psinα−Fmsm=mgsinα−μmgcosαm=gsinα−μgcosα=10.0,4−0,2.10.214=2,167m/s2
b.
Vận tốc tại chân mặt phẳng nghiêng là:
v2−v20=2as⇒v=√v20+2as=√0+2.2,167.0,8=1,862m/sv2−v02=2as⇒v=v02+2as=0+2.2,167.0,8=1,862m/s
c.
Thời gian chuyển động trên mặt phẳng nghiêng là:
t=v−v0a=1,862−02,167=0,86st=v−v0a=1,862−02,167=0,86s
d.
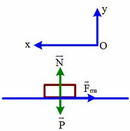
Áp dụng định luật II Niu tơn:
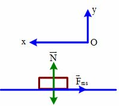
⃗P+⃗Fms+⃗N=m⃗a′+oy:N=P+ox:−Fms=ma′⇒a′=−Fmsm=−μmgm=−μg=−0,2.10=−2m/s2P→+F→ms+N→=ma→′+oy:N=P+ox:−Fms=ma′⇒a′=−Fmsm=−μmgm=−μg=−0,2.10=−2m/s2
e.
Quảng đường tối đa đi được trên mặt phẳng ngang là:
s′=v′2−v22a′=0−1,86222.(−2)=0,8668ms′=v′2−v22a′=0−1,86222.(−2)=0,8668m
f.
Thời gian chuyển động trên mặt phẳng ngang là:
t′=v′−va′=0−1,862−2=0,931s