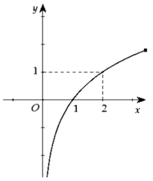
Cho hàm số f(x) xác định và có đạo hàm f'(x) liên tục trên đoạn 1 ; 3 , f x ≠ 0 với mọi x ∈ 1 ; 3 , đồng thời f ' x 1 + f x 2 = f x 2 x − 1 2 v à f 1 = − 1 . Biết rằng ∫ 1 3 f x d x = a ln 3 + b a , b ∈ ℤ , tính tổng S = a + b 2 .
A. S = 2
B. S = 0
C. S = 4
D. S = -1




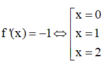
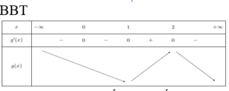
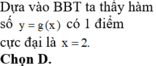
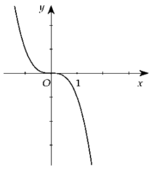


⇒ ∫ 1 x f ' x 1 + f x 2 f x 4 d x = ∫ 1 x x − 1 2 d x , ∀ x ∈ 1 ; 3 ⇔ ∫ 1 x 1 f x 4 + 2 f x 3 + 1 f x 2 d f x = x − 1 3 3 x 1 ⇔ − 1 3 f x 3 − 2 2 f x 2 − 1 f x x 1 = x − 1 3 3 − 0 3 ⇔ − 1 3 f x 3 − 2 2 f x 2 − 1 f x − − 1 3 f 1 3 − 2 2 f 1 2 − 1 f 1 = x − 1 3 3 ⇔ − 1 3 f x 3 − 2 2 f x 2 − 1 f x − 1 3 − 1 + 1 = x − 1 3 3 ⇔ − 1 3 f x 3 − 2 2 f x 2 − 1 f x = x − 1 3 + 1 3 ⇔ 1 3 − 1 f x 3 − − 1 f x 2 + − 1 f x = 1 3 x 3 − x 2 + x ( * )