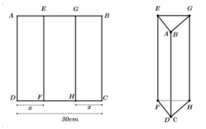
Cho môt tấm tôn hình chữ: nhật ABCD có AD=60cm Ta gấp tấm tôn theo 2 cạnh MN và QP vào phía trong sao cho trùng với (như hình vẽ) để được lăng trụ đứng khuyết hai đáy. Khối lăng trụ có thể tích lớn nhất khi x bằng bao nhiêu
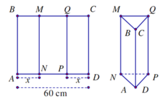
A. x=20
B. =30
C. x=45
D. x=40

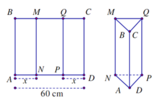
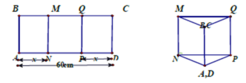

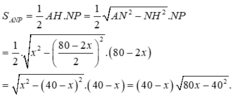

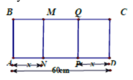
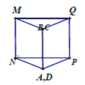

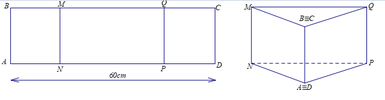

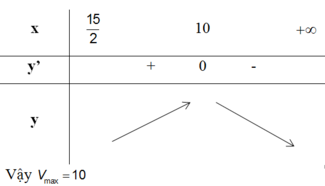
Đáp án A
Thể tích lớn nhất khi diện tích tam giác NPD là lớn nhất, điều này xảy ra khi tam giác đó là tam giác đều (vì chu vi là không đổi) tức là x=20cm