Gọi M và P lần lượt là các điểm biểu diễn các số phức z = x + yi x , y ∈ ℝ , và w = z 2 . Tìm tập hợp các điểm P khi M thuộc đường thẳng d: y = 3x
A. y = − 5 x 2
B. y = − 3 4 x , x ≤ 0
C. y = − 3 4 x
D. y = − 6 5 x , x ≤ 0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Đặt ![]()
![]()
Ta có:![]()
![]()
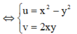
Mà M thuộc đường thẳng d: y = 3x , nên tọa độ của P thỏa mãn
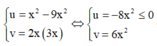
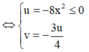
Vậy tập hợp các điểm P là đường thẳng y = - 3 4 x , x ≤ 0

Đáp án B
Số phức liên hợp z ¯ = x − y i . Vậy điểm M′ biểu diễn z ¯ có được bằng cách lấy đối xứng z qua trục hoành.

Số phức z = x + y i x , y ∈ ℝ có tập hợp điểm biểu diễn trên mặt phẳng tọa độ là đường tròn có phương trình
( C ) : x - 1 2 + y - 2 2 = 4 ⇒ - 1 ≤ x ≤ 3
w = z + z ¯ + 2 i = x + y i + x - y i + 2 i = 2 x + 2 i
Tọa độ điểm biểu diễn số phức w là M ( x ; 2 ) , x ∈ - 1 ; 3
Vậy, tập hợp các điểm biểu diễn của số phức là w là đoạn thẳng AB với A(-1;2),B(3;2)
Chọn đáp án B.

\(M\left(1;1\right)\) ; \(N\left(2;3\right)\)
Gọi \(w=x+yi\Rightarrow Q\left(x;y\right)\)
\(\left\{{}\begin{matrix}\overrightarrow{MN}=\left(1;2\right)\\\overrightarrow{MQ}=\left(x-1;y-1\right)\end{matrix}\right.\) \(\Rightarrow\overrightarrow{MN}+3\overrightarrow{MQ}=\left(3x-2;3y-1\right)=0\)
\(\Rightarrow\left\{{}\begin{matrix}x=\dfrac{2}{3}\\y=\dfrac{1}{3}\end{matrix}\right.\) \(\Rightarrow w=\dfrac{2}{3}+\dfrac{1}{3}i\)
Đáp án B
Mà M thuộc đường thẳng d: y = 3x , nên tọa độ của P thỏa mãn
Vậy tập hợp các điểm P là đường thẳng y = − 3 4 x , x ≤ 0