Cho hình chóp tam giác S.ABC có A S C ⏜ = C S B ⏜ = 60 ° , A S C ⏜ = 90 ° , S A = S B = a , S C = 3 a Tính thể tích của khối chóp S.ABC?
A. a 3 2 8 .
B. a 3 2 4 .
C. a 3 2 12 .
D. a 3 2 3 .
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
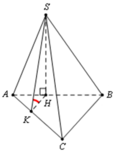
Kẻ H K ⊥ A C K ∈ A C ⇒ S A C ; A B C ^ = S K H ^ = 60 °
ta có A B = 3 A H ⇒ H K = 1 3 d B ; A C = 1 3 a 3 2 = a 3 6
tam giác SHK vuông tại H, có S H = tan S K H ^ . H K = a 2
vậy thể tích khối chóp S.ABC là V = 1 3 S H . S A B C = 1 3 . a 2 . a 2 3 4 = a 3 3 24

Đáp án C.
Hướng dẫn giải: Gọi H là trung điểm AC.
Do tam giác ABC vuông tại B nên H là tâm đường tròn ngoại tiếp tam giác ABC.
Đỉnh S cách đều các điểm A, B,C nên hình chiếu của S trên mặt đáy (ABC) trùng với tâm đường tròn ngoại tiếp tam giác ABC
suy ra S H ⊥ ( A B C )
![]()
Tam giác vuông SBH, có
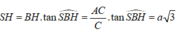
Tam giác vuông ABC ,
có A B = A C 2 - B C 2 = a 3
Diện tích tam giác vuông
S ∆ A B C = 1 2 B A . B C = a 3 2 2
Vậy V S . A B C = 1 3 S ∆ A B C . S H = a 3 2

Đáp án D
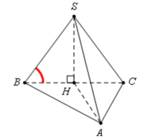
Ta có S H ⊥ A B C ⇒ S B ; A B C ^ = S B ; B C ^ = S B C ^ = 60 °
Tam giác SBH vuông tại H, có S H = tan 60 ° . B H = a 3
Và S A B C = 1 2 . A B . A C = a 2 3 2 .
Vậy thể tích khối chóp là V S . A B C D = 1 3 . S H . S A B C = 1 3 a 3 a 2 3 2 = a 3 2

Chọn C.
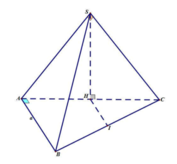
Gọi H, I lần lượt là trung điểm của BC, AC.
Tam giác SAC vuông cân tại S
Tam giác ABC vuông tại A => IA= IB = IC (1).
Lại có:
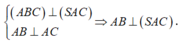
Mà HI là đường trung bình của tam giác ABC
![]()
![]()
![]()
Do đó: I là tâm mặt cầu ngoại tiếp hình chóp S.ABC
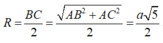
Vậy diện tích mặt cầu là
![]()
Đáp án B
Công thức tính thể tích hình chóp tam giác biết độ dài các cạnh bên a , b , c và các góc tạo bởi các cạnh bên là α , β , γ như sau:
V = a b c 6 1 − cos 2 α − cos 2 β − cos 2 γ + 2 cos α cos β cos γ
= 3 a 3 6 1 − cos 2 60 − cos 2 60 − cos 2 90 + 2 cos 60 cos 60 cos γ 90 = a 3 2 4