Cho hình lăng trụ tam giác đều A B C . A ' B ' C ' có A B = 2 3 và AA' = 2 Gọi M, N, P lần lượt là trung điểm của các cạnh A'B', A'C' và BC. Côsin của góc tạo bởi hai mặt phẳng (AB'C') và (MNP) bằng:
A. 6 13 65 .
B. 13 65 .
C. 17 13 65 .
D. 18 63 65 .


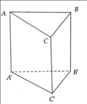


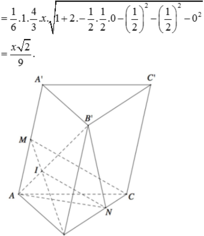
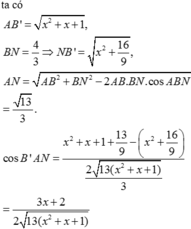
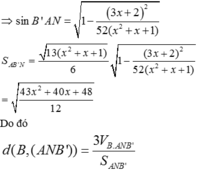
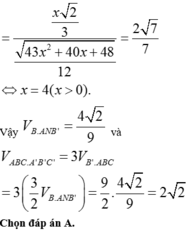

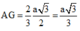
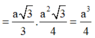
Đáp án B