Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
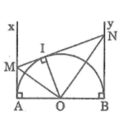
Gọi I là tiếp điểm của tiếp tuyến MN với đường tròn (O). Nối OI
Ta có: 
(hai góc kề bù)
OM là tia phân giác của góc AOI (tính chất hai tiếp tuyến cắt nhau)
ON là tia phân giác của góc BOI (tính chất hai tiếp tuyến cắt nhau)
Suy ra : OM ⊥ ON (tính chất hai góc kề bù)
Vậy 
a) x4+x3+2x2+x+1=(x4+x3+x2
)+(x2+x+1)=x2
(x2+x+1)+(x2+x+1)=(x2+x+1)(x2+1)
b)a3+b3+c3
-3abc=a3+3ab(a+b)+b3+c3
-(3ab(a+b)+3abc)=(a+b)3+c3
-3ab(a+b+c)
=(a+b+c)((a+b)2
-(a+b)c+c2
)-3ab(a+b+c)=(a+b+c)(a2+2ab+b2
-ac-ab+c2
-3ab)=(a+b+c)(a2+b2+c2
-ab-ac-bc)
c)Đặt x-y=a;y-z=b;z-x=c
a+b+c=x-y-z+z-x=o
đưa về như bài b
d)nhóm 2 hạng tử đầu lại và 2hangj tử sau lại để 2 hạng tử sau ở trong ngoặc sau đó áp dụng hằng đẳng thức dề tính sau đó dặt nhân tử chung
e)x2
(y-z)+y2
(z-x)+z2
(x-y)=x2
(y-z)-y2
((y-z)+(x-y))+z2
(x-y)
=x2
(y-z)-y2
(y-z)-y2
(x-y)+z2
(x-y)=(y-z)(x2
-y2
)-(x-y)(y2
-z2
)=(y-z)(x2
-2y2+xy+xz+yz)
k mk nha $_$
:D
a) Vì MA , MI là 2tt của đường tròn (O) , nên ^O1 = ^O2 (1)
Vì NB , NI là 2tt của nửa đường tròn (O) , nên ^O3 = ^O4 (2)
Từ (1) và (2) => \(\widehat{O_2}+\widehat{O_3}=\widehat{O_1}+\widehat{O_4}=\frac{180^o}{2}=90^o\)
Mà ^MON = 90^o
Vậy : ^MON = 90^o
b) Theo t/c 2tt cắt nhau , ta có :
AM = MI ; NI = NB
MN = MI + IN = AM + BN
Vậy : MN = AM + BN ( đpcm )
c) Áp dụng hệ thức lượng tam giác trong tam giác OMN vuông tại O , đường cao OI
Ta có : \(OI^2=IM.IN\)
\(\Rightarrow IM.IN=R^2\)( R bán kính )
Mặt khác : MA = MI ; NB = NT
Vậy : AM . BN = R^2 ( đpcm )
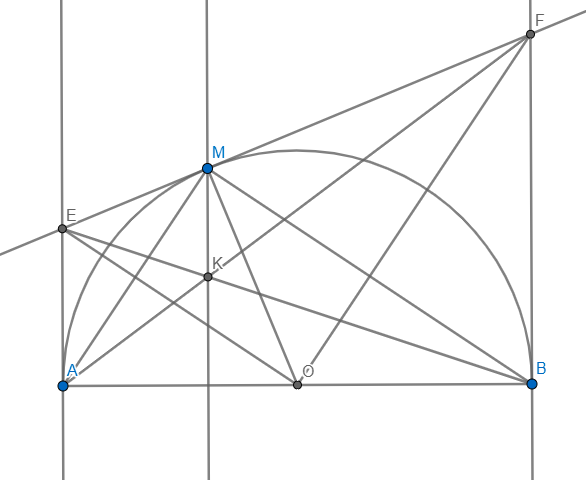
1) Vì EM,EA là tiếp tuyến \(\Rightarrow OE\) là phân giác \(\angle MOA\)
\(\Rightarrow\angle MOE=\dfrac{1}{2}\angle MOA\)
Vì FM,FB là tiếp tuyến \(\Rightarrow OF\) là phân giác \(\angle MOB\)
\(\Rightarrow\angle MOF=\dfrac{1}{2}\angle MOB\)
\(\Rightarrow\angle MOE+\angle MOF=\dfrac{1}{2}\left(\angle MOA+\angle MOB\right)=\dfrac{1}{2}.180=90\)
\(\Rightarrow\angle EOF=90\)
2) Ta có: \(\angle EAO+\angle EMO=90+90=180\Rightarrow AEMO\) nội tiếp
\(\Rightarrow\angle MEO=\angle MAO\)
Vì AB là đường kính \(\Rightarrow\angle AMB=90\)
Xét \(\Delta MAB\) và \(\Delta OEF:\) Ta có: \(\left\{{}\begin{matrix}\angle AMB=\angle EOF\\\angle FEO=\angle MAB\end{matrix}\right.\)
\(\Rightarrow\Delta MAB\sim\Delta OEF\left(g-g\right)\)
Vì \(AE\parallel BF(\bot AB)\) \(\Rightarrow\dfrac{BF}{AE}=\dfrac{FK}{AK}\left(1\right)\)
Vì EM,EA là tiếp tuyến \(\Rightarrow EA=EM\left(2\right)\)
Vì FM,FB là tiếp tuyến \(\Rightarrow FB=FM\left(3\right)\)
Thế (2),(3) vào (1) \(\Rightarrow\dfrac{FM}{EM}=\dfrac{FK}{AK}\Rightarrow\) \(MK\parallel AE\) \(\Rightarrow MK\bot AB\)
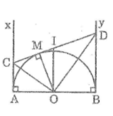
Theo tính chất tiếp tuyến, ta có:
Ax ⊥ AB
By ⊥ AB
Suy ra: Ax // By hay AC // BD
Suy ra tứ giác ABDC là hình thang
Gọi I là trung điểm của CD
Khi đó OI là đường trung bình của hình thang ABDC
Suy ra: OI // AC ⇒ OI ⊥ AB
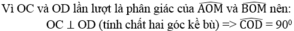
Suy ra: IC = ID = IO = (1/2).CD (tính chất tam giác vuông)
Suy ra I là tâm đường tròn đường kính CD. Khi đó O nằm trên đường tròn tâm I đường kính CD và IO vuông góc với AB tại O.
Vậy đường tròn có đường kính CD tiếp xúc với AB tại O.
a) Xét (O) có
CM là tiếp tuyến có M là tiếp điểm(gt)
CA là tiếp tuyến có A là tiếp điểm(gt)
Do đó: OC là tia phân giác của \(\widehat{AOM}\)(Tính chất hai tiếp tuyến cắt nhau)
nên \(\widehat{AOM}=2\cdot\widehat{COM}\)
Xét (O) có
DB là tiếp tuyến có B là tiếp điểm(gt)
DM là tiếp tuyến có M là tiếp điểm(gt)
Do đó: OD là tia phân giác của \(\widehat{MOB}\)(Tính chất hai tiếp tuyến cắt nhau)
nên \(\widehat{BOM}=2\cdot\widehat{DOM}\)
Ta có: \(\widehat{AOM}+\widehat{BOM}=180^0\)(hai góc kề bù)
mà \(\widehat{AOM}=2\cdot\widehat{COM}\)(cmt)
và \(\widehat{BOM}=2\cdot\widehat{DOM}\)(cmt)
nên \(2\cdot\widehat{DOM}+2\cdot\widehat{COM}=180^0\)
\(\Leftrightarrow2\cdot\left(\widehat{DOM}+\widehat{COM}\right)=180^0\)
\(\Leftrightarrow\widehat{DOM}+\widehat{COM}=90^0\)
mà \(\widehat{DOM}+\widehat{COM}=\widehat{COD}\)(tia OM nằm giữa hai tia OC, OD)
nên \(\widehat{COD}=90^0\)
Vậy: \(\widehat{COD}=90^0\)
b) Gọi E là trung điểm của CD
Xét ΔCOD có \(\widehat{COD}=90^0\)(cmt)
nên ΔCOD vuông tại O(Định nghĩa tam giác vuông)
Xét ΔCOD cân tại O(cmt) có OE là đường trung tuyến ứng với cạnh huyền CD(E là trung điểm của CD)
nên \(OE=\dfrac{CD}{2}\)(Định lí 1 về áp dụng hình chữ nhật vào tam giác vuông)
mà \(CE=ED=\dfrac{CD}{2}\)(E là trung điểm của CD)
nên EO=EC=ED
⇒O∈(E)
Ta có: AC⊥AB(AC là tiếp tuyến có A là tiếp điểm của (O))
BD⊥BA(BD là tiếp tuyến có B là tiếp điểm của (O))
Do đó: AC//BD(Định lí 1 từ vuông góc tới song song)
Xét tứ giác ACDB có AC//DB(cmt)
nên ACDB là hình thang có hai đáy là AC và DB(Định nghĩa hình thang)
Xét (O) có AB là đường kính(gt)
nên O là trung điểm của AB
Xét hình thang ACDB(AC//DB) có
E là trung điểm của CD(gt)
O là trung điểm của AB(cmt)
Do đó: OE là đường trung bình của hình thang ACDB(Định nghĩa đường trung bình của hình thang)
⇒OE//AC//DB và \(OE=\dfrac{AC+DB}{2}\)(Định lí 4 về đường trung bình của hình thang)
Ta có: OE//AC(cmt)
AC⊥AB(AC là tiếp tuyến có A là tiếp điểm của (O))
Do đó: OE⊥AB(Định lí 2 từ vuông góc tới song song)
mà O∈AB(O là trung điểm của AB)
nên OB⊥OE tại O
Xét (E) có
O∈(E)(cmt)
OB⊥OE tại O(cmt)
Do đó: OB là tiếp tuyến của (E)(Dấu hiệu nhận biết tiếp tuyến của đường tròn)
⇔AB là tiếp tuyến của (E)
hay đường tròn đường kính CD tiếp xúc với AB(Đpcm)
