Cho hàm số y = f(x) có đổ thị như hình vẽ bên. Biết rằng f(x) là một trong bốn hàm số được đưa ra trong các phương án A, B, C, D dưới đây. Tìm f(x)
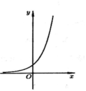
A . f ( x ) = e x
B . f ( x ) = ( 3 π ) x
C . f ( x ) = ln x
D . f ( x ) = x e π
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C.
Hàm số có hai cực trị → loại A, B (vì hàm phân thức không có cực trị, hàm trùng phương số cực trị là 1 hoặc 3).
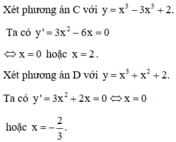
Dựa vào đồ thị ta có hai điểm cực trị có hoành độ đều không âm.

Chọn D
Ta có

Vì f'(x) luôn đồng biến trên
ℝ
nên ![]() , do đó: a > 0 và b > 0
, do đó: a > 0 và b > 0
Mặt khác vì đồ thị hàm số không cắt trục Ox nên chọn đáp án D.

Ta có bảng biến thiên như hình vẽ sau:
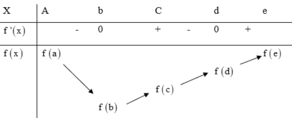
Giá trị nhỏ nhất của hàm số là f( b) nhưng giá trị lớn nhất có thể là f (a) hoặc f( e) Theo giả thiết ta có: f(a) + f( c)) = f( b) + f( d) nên f(a) - f( d)) = f( b) - f( c)< 0
Suy ra : f( a) < f( d) < f( e)
Vậy m a x [ a ; e ] f ( x ) = f ( e ) ; m i n [ a ; e ] f ( x ) = f ( b )
Chọn C.

Chọn C
Trên đoạn [ - 1; 1] đồ thị hàm số y= f’( x) nằm phía trên trục hoành.
=> Trên đoạn [ - 1; 1] thì f’( x) > 0.
=> Trên đoạn [ - 1; 1] thì hàm số y= f( x) đồng biến