Cho hàm số y = x 4 − 4 x 2 + 3 có đồ thị (C). Có bao nhiêu điểm trên trục tung từ đó có thể vẽ được 3 tiếp tuyến đến đồ thị (C)
A. 3
B. 2
C. 1
D. 0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
19 tháng 8 2018
Đáp án C
Phương pháp giải: Lập phương trình tiếp tuyến với hệ số góc k và đi qua điểm thuộc Oy, sử dụng điều kiện để hai đồ thị tiếp xúc tìm tham số m
CM
27 tháng 9 2018
+ Ta có y ' = f ' ( x ) = a d - b c ( c x + d ) 2 . Từ đồ thị hàm số y= f’(x) ta thấy:
Đồ thị hàm số y= f’(x) có tiệm cận đứng x=1 nên –d/c= 1 hay c= -d
Đồ thị hàm số y= f’(x ) đi qua điểm (2;2)
⇒ a d - b c ( 2 c + d ) 2 = 2 ↔ a d - b c = 2 ( 2 c + d ) 2
Đồ thị hàm số y= f’(x) đi qua điểm (0;2)
⇒ a d - b c d 2 = 2 ↔ a d - b c = 2 d 2
Đồ thị hàm số y=f(x) đi qua điểm (0;3) nên b/d= 3 hay b= 3d
Giải hệ gồm 4 pt này ta được a=c= -d và b= 3d .
Ta chọn a=c= 1 ; b= -3 ; d= -1
⇒ y = x - 3 x - 1
Chọn D.
27 tháng 4 2016
Xét \(M\left(0;m\right)\in Oy\). Đường thẳng d đi qua M, hệ số góc k có phương trình : \(y=kx+m\)
d là tiếp tuyến \(\Leftrightarrow\begin{cases}x^4-2x^2-1=kx+m\\4x^3-4x=k\end{cases}\) có nghiệm
Thế k vào phương trình thứ nhất, ta được :
\(-x^4-2x^2-1=4x^4-4x^2+m\)
\(\Leftrightarrow5x^4-2x^2+1+m=0\) (*)
Để từ M ta có thể kẻ đến đồ thị đúng 3 tiếp tuyến \(\Leftrightarrow\) (*) có 3 nghiệm phân biệt \(\Leftrightarrow m+1=0\Leftrightarrow m=-1\)
Khi đó (*) có 3 nghiệm \(x=0;x=\pm\sqrt{\frac{2}{5}}\) và 3 tiếp tuyến đó là :
\(y=-1;y=\pm\sqrt{\frac{2}{5}}x-1\)
Vậy \(M\left(0;-1\right)\) là điểm cần tìm
CM
28 tháng 10 2018
Đáp án B.
Gọi A 0 ; a là điểm trên trục tung thỏa mãn yêu cầu đề bài.
Gọi k là hệ số góc tiếp tuyến đi qua A.
Lúc này ta có hệ
x 4 − x 2 + 1 = k x − 0 + a 4 x 3 − 2 x = k ⇒ x 4 − x 2 + 1 = 4 x 3 − 2 x x + a
⇔ 3 x 4 − x 2 + a − 1 = 0 (*).
Để từ A kẻ được ba tiếp tuyến khác nhau trên đồ thị hàm số y = x 4 − x 2 + 1 thì phương trình (*) phải có đúng 3 nghiệm phân biệt.
Điều này xảy ra khi và chỉ khi phương trình (*) có 1 nghiệm bằng 0 và 1 nghiệm dương ⇔ a = 1 . Vậy có duy nhất một điểm trên trục tung thỏa mãn yêu cầu đề bài.
CM
14 tháng 6 2017
Chọn đáp án C
Tập xác định: D = R.
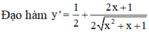
Gọi ∆ là đường thẳng đi qua M 0 ; m và có hệ số góc là k, phương trình đường thẳng ∆ : y = k x + m .
Đường thẳng ∆ là tiếp tuyến của (C) khi và chỉ khi hệ phương trình sau có nghiệm :
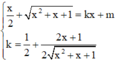
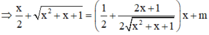
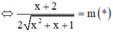
Hệ phương trình trên có nghiệm khi và chỉ khi phương trình (*) có nghiệm
Xét hàm số f x = x + 2 2 x 2 + x + 1 trên R.
Đạo hàm
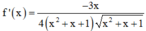
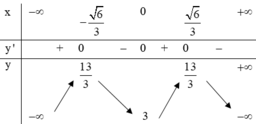
Bảng biến thiên
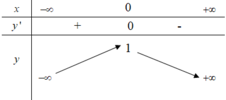
Dựa vào bảng biến thiên ta thấy: Phương trình (*) có nghiệm
⇔ - 1 2 < m ≤ - 1 hay m ∈ ( - 1 2 ; 1 ] .
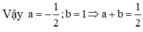
Đáp án C