Cho hình chóp S.ABCD có tất cả các cạnh bên và cạnh đáy đều bằng a và ABCD là hình vuông.Gọi M là trung điểm của CD Giá trị M S → . C B → bằng:
A. a 2 2
B. − a 2 2
C. a 2 3
D. 2 a 2 2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
MN là đường trung bình của tam giác DAS nên MN//SA.
Gọi O là tâm của hình vuông ABCD, vì SA=SC=SB=SD nên
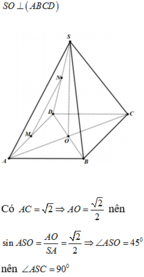

Đáp án C
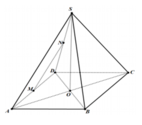
MN là đường trung bình của tam giác DAS nên MN//SA
Gọi O là tâm của hình vuông ABCD, vì SA=SC=SB=SD nên SO ⊥ (ABCD)
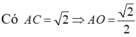
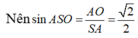
![]()

đáp án D
Do S.ABCD là hình chóp tứ giác đều ⇒ S O ⊥ ( A B C D ) .
Gọi K là trung điểm OD
MK sẽ là đường trung bình trong tam giác ∆ S O D
⇒ M K ⊥ ( A B C D )
![]()
⇒ tan M B K = M K B K

![]()
⇒ tan M B K = M K B K = 1 3
Chọn đáp án D
Đáp án A
Gọi O là tâm của hình vuông, ta có
M S → . C B → = M S → .2 M O → = 2. ( M O → + O C → ) . M O → = 2 M O 2 + 0 = a 2 2