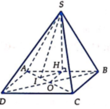
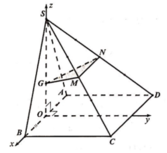
Cho hình chóp S.ABCD có đáy là hình vuông, gọi M là trung điểm của AB. Tam giác SAB cân tại S và nằm trong mặt phẳng vuông góc với đáy. Biết SD = a 3 , SC tạo với mặt phẳng đáy (ABCD) một góc Thể tích khối chóp S.ABCD theo a là
A. 4 a 3 3 .
B. 3 a 3 10 .
C. 4 a 3 15 5 .
D. 2 a 3 15 3 .

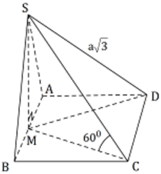
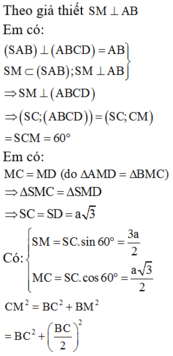
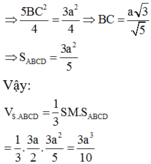
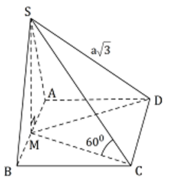
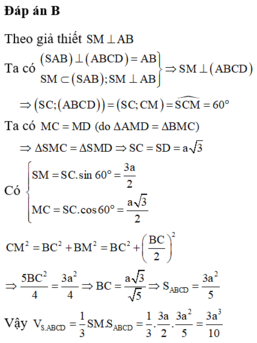


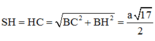
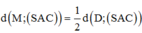
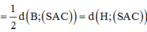
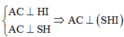
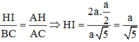
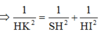
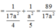
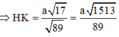
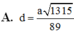
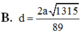
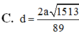
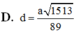

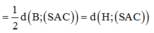

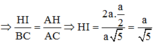
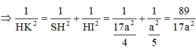
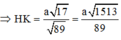
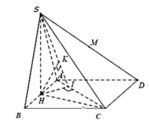

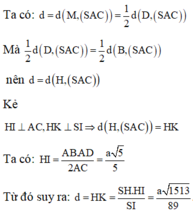
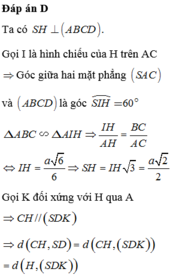

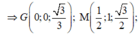
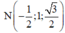
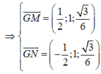
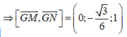
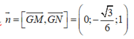
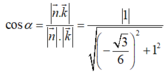
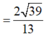
Đáp án B