Cho hình chóp S.ABCD có đáy ABCD là hình thang vuống tại A và D có
A
B
=
2
A
D
=
2
C
D
.
Tam giác SAD đều và nằm trong mặt phẳng vuống góc với đáy. Gọi I là trung điểm AD. Biết khoảng cách từ I đến mặt phẳng (SBD) bằng 1cm Tính diện tích hình thang ABCD. A.
S
=
200
27
c
m
2
B.
S
=
10
3
c
m
2
...
Đọc tiếp
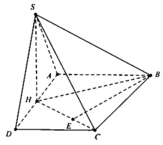
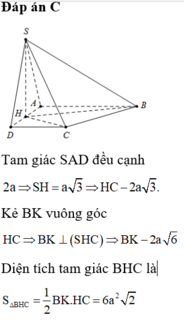
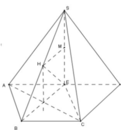
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuống tại A và D có A B = 2 A D = 2 C D . Tam giác SAD đều và nằm trong mặt phẳng vuống góc với đáy. Gọi I là trung điểm AD. Biết khoảng cách từ I đến mặt phẳng (SBD) bằng 1cm Tính diện tích hình thang ABCD.
A. S = 200 27 c m 2
B. S = 10 3 c m 2
C. S = 5 3 c m 2
D. S = 19 2 c m 2
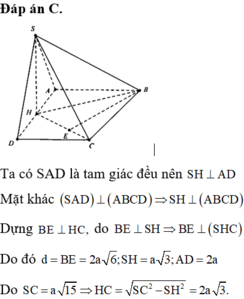
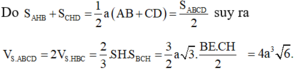
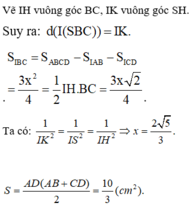
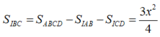
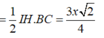
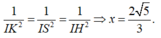
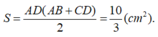
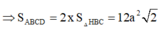
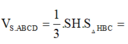
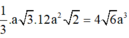
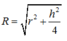
Đáp án D
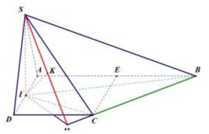
Đặt A D = x x > 0 . Gọi J là trung điểm BD ta có IS ⊥ I D ; I S ⊥ I J ; I D ⊥ I J .
Tứ diện SIJD vuông tại I. Gọi h là khoảng cách từ I đến mặt phẳng S B D ta có.
1 = 1 h 2 = 1 S I 2 + 1 I D 2 + 1 I J 2 = 1 x 3 2 2 + 1 x 2 2 + 1 x 2 2 + 1 x ⇒ h = 57 19 x .
Từ giả thiết ⇒ x = 57 3 c m
Vậy S A B C D = 1 2 A B + D C . A D = 19 2