Tổng tất cả các số n thỏa mãn C n 1 + C n 2 ≥ C n 3 (trong đó C n k là tổ hợp chập k của n phần tử) là
A. 24.
B. 23.
C. 31.
D. 18.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
4 tháng 6 2019
Đáp án D
Số các tổ hợp chập k của một tập hợp có n phần tử với 1 ≤ k ≤ n là C n k = n ! k ! n − k ! = A n k k !
CM
9 tháng 5 2019
Điều kiện: n - 1 ≥ 4 nên n ≥ 5
Hệ điều kiện ban đầu tương đương:
⇔ n - 1 n - 2 n - 3 n - 4 4 . 3 . 2 . 1 - n - 1 n - 2 n - 3 3 . 2 . 1 ≤ 5 4 n - 2 n - 3 n + 1 n n - 1 n - 2 n - 3 5 . 4 . 3 . 2 . 1 ≥ 7 15 n + 1 n n - 1 ⇔ n 2 - 9 n - 22 < 0 n ≥ 5 n 2 - 5 n - 50 ≥ 0 ⇒ n = 10
Vậy n = 10 thỏa yêu cầu bài toán
Đáp án D
CM
14 tháng 12 2018
Đáp án D
Phương pháp: Chỉnh hợp chập k của tập hợp có n phần tử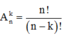 
Cách giải:
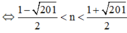
Mà 
Thay lần lượt n = 2;3;4;5;6;7 vào 
n |
2 |
3 |
4 |
5 |
6 |
7 |
k |
Loại |
Loại |
Loại |
Loại |
Loại |
Loại |
Vậy n = 5
Khi đó, 
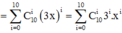
Số hạng chứa
x
5
trong khai triển ứng với i = 5. Số hạng đó là: 
Đáp án D