Cho hai điểm A,B cố định, A B = 1 . Tập hợp các điểm M trong không gian sao cho diện tích tam giác MAB bằng 4 là một mặt trụ. Tính bán kính r của mặt trụ đó.
A. r = 4
B. r = 2
C. r = 1
D. r = 8
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
26 tháng 5 2017
Đáp án D
Ta có
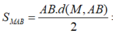
Vậy M thuộc mặt trụ có trục AB và bán kính r = 8
CM
16 tháng 12 2019
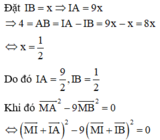
⇔ M I 2 + 2 M I → . I A → + I A 2 − 9 M I 2 + 2 M I → . I B → + I B 2 = 0 ⇔ M I 2 + I A 2 − 9 M I 2 − 9 I B 2 + 2 M I → I A → − 9 I B → = 0 ⇔ − 8 M I 2 + I A 2 − 9 I B 2 = 0 ⇒ − 8 M I 2 + 9 2 2 − 9. 1 2 2 = 0 ⇔ − 8 M I 2 = − 18 ⇔ M I 2 = 9 4 ⇔ M I = 3 2
Vậy M nằm trên mặt cầu tâm I bán kính M I = 3 2
Chọn: D
CM
13 tháng 10 2019
Chọn D
Gọi E, F là các điểm chia trong và chia ngoài của đoạn thẳng AB theo tỉ số 3, nghĩa là
Khi đó, E , F là chân các đường phân giác trong và phân giác ngoài của góc M của tam giác MAB. Suy ra:
Vậy M thuộc mặt cầu đường kính EF. Tính được EF = 3, suy ra R=3/2
20 tháng 12 2019
a) Xét tứ giác BEDC có:
∠BEC = 90o (CE là đường cao)
∠BDC = 90o (BD là đường cao)
=> Hai đỉnh D và E cùng nhìn cạnh BC dưới 1 góc vuông
=> Tứ giác BEDC là tứ giác nội tiếp
b) Xét ΔAEC và ΔADB có:
∠BAC là góc chung
∠AEC = ∠BDA = 90o
=> ΔAEC ∼ ΔADB (g.g)
\(\Rightarrow\frac{AE}{AD}=\frac{AC}{AB}\Rightarrow\text{AE.AB = AC.AD}\)
c) Ta có:
∠FBA = 90o (góc nội tiếp chắn nửa đường tròn)
=>FB⊥AB
Lại có: CH⊥AB (CH là đường cao)
=> CH // FB
Tương tự,( FCA) = 90o (góc nội tiếp chắn nửa đường tròn)
=>FC⊥AC
BH là đường cao => BH ⊥AC
=> FC // BH
Xét tứ giác CFBH có:
CH // FB
FC // BH
=> Tứ giác CFBH là hình bình hành.
Mà I là trung điểm của BC
=> I cũng là trung điểm của FH
Hay F, I, H thẳng hàng.
2) Diện tích xung quanh của hình trụ:
S = 2πRh = 2πR2 = 128π (do chiều cao bằng bán kính đáy)
=> R = 8 cm ; h = 8cm
Thể tích của hình trụ là
V = πR2 h = π.82.8 = 512π (cm3)
HÌNH TRONG THỐNG KÊ HỎI ĐÁP NHA VỚI LẠI MIK TRẢ LỜI TOÀN CÂU KHÓ MÀ CHẲNG CÓ CÁI GP NÀO
CM
24 tháng 6 2019
Xét mệnh đề (I):
Gọi I, J lần lượt là trung điểm AB, CD. Khi đó
M A → + M B → = M C → + M D → ⇔ 2 M I → = 2 M J → ⇔ M I = M J
Do đó tập hợp các điểm M là mặt phẳng trung trực của IJ
Vậy mệnh đề này đúng.
* Xét mệnh đề (II):
Gọi G là trọng tâm tứ diện ABCD
Khi đó M A → + M B → + M C → + M D → = 4 ⇔ 4 M G → = 4 ⇔ M G = 1
Do đó tập hợp các điểm M là mặt cầu tâm G ( 1;2;3 ) và bán kính R = 1
Vậy mệnh đề này đúng
Đáp án D
Đáp án đúng : D