Số điểm cực trị của hàm số y = sin x - π 4 ; x ∈ - π ; π là:
A. 2
B. 4
C. 3
D. 5
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đặt \(sinx=t\Rightarrow t\in\left[-\dfrac{1}{2};1\right]\)
\(y=f\left(t\right)=2t^2+t+4\)
Xét hàm \(f\left(t\right)=2t^2+t+4\) trên \(\left[-\dfrac{1}{2};1\right]\)
\(-\dfrac{b}{2a}=-\dfrac{1}{4}\in\left[-\dfrac{1}{2};1\right]\)
\(f\left(-\dfrac{1}{2}\right)=4\) ; \(f\left(-\dfrac{1}{4}\right)=\dfrac{31}{8}\); \(f\left(1\right)=7\)
\(y_{max}=7\) khi \(t=1\) hay \(x=\dfrac{\pi}{2}\)
\(y_{min}=\dfrac{31}{8}\) khi \(sinx=-\dfrac{1}{4}\)

y = \(\dfrac{sin^2x}{cosx\left(sinx-cosx\right)}+\dfrac{1}{4}\)
y = \(\dfrac{sin^2x}{sinx.cosx-cos^2x}+\dfrac{1}{4}=\dfrac{\dfrac{sin^2x}{cos^2x}}{\dfrac{sinx.cosx}{cos^2x}-1}+\dfrac{1}{4}\)
y = \(\dfrac{tan^2x}{tanx-1}+\dfrac{1}{4}\)
y = \(\dfrac{4tan^2x+tanx-1}{4tanx-4}\). Đặt t = tanx. Do x ∈ \(\left(\dfrac{\pi}{4};\dfrac{\pi}{2}\right)\) nên t ∈ (1 ; +\(\infty\))\
Ta đươc hàm số f(t) = \(\dfrac{4t^2+t-1}{4t-4}\)
⇒ ymin = \(\dfrac{17}{4}\) khi t = 2. hay x = arctan(2) + kπ

Đáp án D.
Ta có: y’ = cos 3x + mcos x
Hàm số đạt cực đại tại
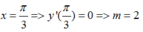
m = 2 => y’ = cos 3x + 2cos x => y’’ = -3sin 3x – 2sin x
=>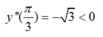
Vậy, m = 2

Chọn B.
Phương pháp : Sử dụng đạo hàm và xét dấu đạo hàm để tìm cực trị.
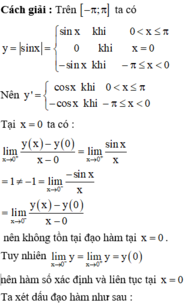
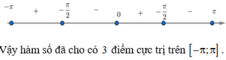
Xét hàm số
Bảng biến thiên:
Do y = sin x - x 4 là hàm lẻ nên đồ thị hàm số y = sin x - x 4 nhận O(0;0) là tâm đối xứng.
Đồ thị hàm số cắt trục Ox tại 3 điểm phân biệt x 1 ; x 2 ; x 3 ( x 1 ; x 2 ; x 3 khác ± x 0 )
Số điểm cực trị của hàm số số y = sin x - π 4 ; x ∈ - π ; π là: 2 + 2 = 4
Chọn B.