Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
- Dùng quỳ tím
+) Hóa đỏ: H2SO4
+) Hóa xanh: NaOH
+) Không đổi màu: NaCl và nước cất
- Đổ dd AgNO3 vào 2 lọ còn lại
+) Xuất hiện kết tủa: NaCl
PTHH: \(NaCl+AgNO_3\rightarrow NaNO_3+AgCl\downarrow\)
+) Không hiện tượng: Nước cất
- Cho quỳ tím vào các mẫu thử :
+ Quỳ tím chuyển thành màu xanh : Ca(OH)2 ; KOH (I)
+ Quỳ tím chuyển thành màu đỏ : H2SO4
+ Không hiện tượng : NaCl
- Sục khí CO2 qua 2 dd (I)
+ Hiện tượng kết tủa : Ca(OH)2
\(Ca\left(OH\right)_2+CO_2\rightarrow CaCO_3+H_2O\)
+ Không hiện tượng : KOH
(a) CO2 + NaOH → NaHCO3
Dung dịch sau pứ chỉ có NaHCO3
(b) 2NaOH + Ca(HCO3)2 → Na2CO3 + CaCO3 + H2O
Dung dịch sau pứ: (Na2CO3; NaOH dư)
(c) Ba(HCO3)2 + H2SO4 → BaSO4 + 2CO2 + 2H2O
Dung dịch sau pứ: Ba(HCO3)2 dư
(d) Mg + CuSO4 → MgSO4 + Cu
Dung dịch sau pứ: (MgSO4; CuSO4 dư)
(e) Na + H2O → NaOH + ½ H2
NaOH + CH3COOH → CH3COONa + H2O
Dung dịch sau pứ: (NaOH dư; CH3COONa)
(f) Dung dịch sau pứ: (C6H6; Br2/H2O)
Trích mẫu thử
Cho quỳ tím vào các mẫu thử
- mẫu thử nào làm quỳ tím hóa đỏ là H2SO4
- mẫu thử nào làm quỳ tím hóa xanh là NaOH và Ca(OH)2. Gọi là nhóm 1
- mẫu thử nào không đổi màu quỳ tím là NaCl và nước cất. Gọi là nhóm 2
Cho dung dịch axit sunfuric vào nhóm 1
- mẫu thử nào xuất hiện kết tủa trắng là Ca(OH)2
\(Ca(OH)_2 + H_2SO_4 \to CaSO_4 + 2H_2O\)
- mẫu thử nào không hiện tượng là NaOH
Cho dung dịch bạc nitrat vào các mẫu thử nhóm 2
- mẫu thử nào tạo kết tủa trắng là NaCl
\(NaCl + AgNO_3 \to AgCl + NaNO_3\)
- mẫu thử nào không hiện tượng là nước cất
Nước cứng tạm thời là muối của Ca2+ và Mg2+.
Các chất làm mềm nước là: dung dịch Na2CO3, dung dịch Ca(OH)2, dung dịch Na3PO4.
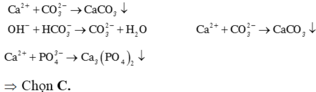
a, \(n_{NaOH}=0,2.1=0,2\left(mol\right)\)
\(m_{NaOH}=0,2.40=8\left(g\right)\)
b, \(n_{H_2SO_4}=2.0,1=0,2\left(mol\right)\)
\(c,C\%=\dfrac{6}{200}.100\%=3\%\)
\(m_{NaCl}=\dfrac{200.8}{100}=16\left(g\right)\)
