Cho hình chóp S.ABC có đường cao SA tam giác ABC là tam giác cân tại A có AB = a, B A C ^ = 120 0 . Biết thể tích khối chóp S.ABC bằng 3 a 3 4 góc giữa hai mặt phẳng (SBC) và (ABC) bằng
A. 90 0
B. 30 0
C. 60 0
D. 45 0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Phương pháp:
Thể tích khối chóp có chiều cao h và diện tích đáy S là V = 1 3 hS
Sử dụng công thức tính diện tích tam giác để tính toán.
Cách giải:
Xét tam giác ABC vuông tại A ta có
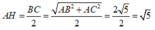
Mà ![]()
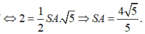
Thể tích khối chóp 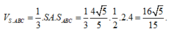
Chọn A.

Đáp án C
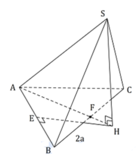
Gọi H là tâm đường tròn ngoại tiếp tam giác ABC bằng cách dựng như hình vẽ.


Đáp án D
Thể tích hình chóp là: V = 1 3 S A . S A B C = 1 3 . a . 1 2 2 a 2 = 2 a 3 3

Đáp án là D
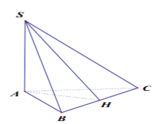
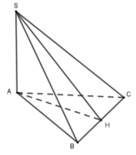
Gọi H là trung điểm của BC, ta có: AH ⊥ BC
Do SA
⊥
(ABC) ![]()
Ta có: ![]()
Xét tam giác vuông SAH:
![]()
![]()
Phương pháp:
Xác định góc giữa các mặt phẳng (P) và (Q) ta thực hiện các bước sau:
+ Xác định giao tuyến d của (P) và (Q)
+ Trong mặt phẳng (P) xác định đường thẳng a ⊥ d trong mặt phẳng (Q) xác định đường thẳng b ⊥ d
+ Khi đó góc giữa (P) và (Q) là góc giữa hai đường thẳng a và b
Cách giải:
Gọi M là trung điểm BC => AM ⊥ BC (do ∆ ABC cân tại A).
Lại có ∆ SAB = ∆ SAC(c.g.c) hay ∆ SBC cân tại S
=> SM ⊥ BC
Theo đề bài
Lại thấy ∆ ABM vuông tại M có AB = a;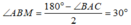
Xét tam giác SAM vuông tại A có SA = AM = a 2 nên ∆ SAM vuông cân tại A hay ∠ S M A = 45 °
Vậy góc giữa (SBC) và (ABC) bằng 45 °
Chọn D.