Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O, cạnh a, góc B A D ^ = 60 ° có SO vuông góc mặt phẳng (ABCD) và SO = a, Khoảng cách từ O đến mặt phẳng (SBC) là
A. a 57 3
B. a 3 4
C. a 57 19
D. 2 a 3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
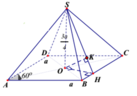
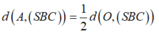
AC cắt (SBC) tại C , O là trung điểm AC =>khoảng cách
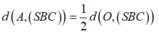
* Trong (ABCD) dựng OH ⊥ BC, trong (SOH) dựng OK ⊥ SH ta chứng minh được OK ⊥ (SBC)
=> khoảng cách d(O,(SBC))= OK.
∆ O B C vuông tại O có OH đường cao
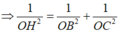
∆ S O H vuông tại O có OK đường cao
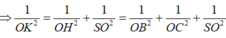
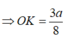
Vậy
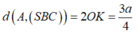

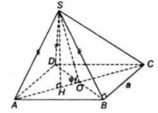
a) Tam giác ABD có AB = AD ( do ABCD là hình thoi)
=> Tam giác ABD cân tại A. Lại có góc A= 60o
=> Tam giác ABD đều.
Lại có; SA = SB = SD nên hình chóp S.ABD là hình chóp đều.
* Gọi H là tâm của tam giác ABD
=>SH ⊥ (ABD)
*Gọi O là giao điểm của AC và BD.
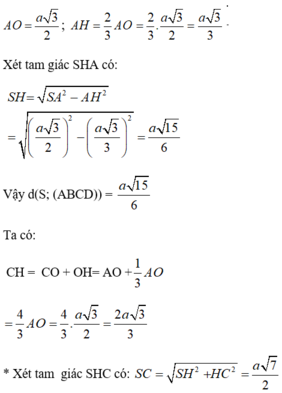

Đáp án C
Kẻ O K ⊥ B C , O H ⊥ S K như hình vẽ khi đó OH là khoảng cách từ O tới (SBC)
Dễ thấy Δ A B D đều
⇒ O K = O B . sin 60 0 = a 2 . 3 2 = a 3 4
Ta có: 1 O H 2 = 1 O K 2 + 1 S O 2 = 16 3 a 2 + 1 a 2 = 19 3 a 2
⇒ O H = a 57 19