Tính giá trị bằng số của biểu thức ln(1/e)
A. 1 B. -1
C. 1/e D. -1/e
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
2 tháng 6 2021
`A=x^2-4x+1`
`=x^2-4x+4-3`
`=(x-2)^2-3>=-3`
Dấu "=" xảy ra khi x=2
`B=4x^2+4x+11`
`=4x^2+4x+1+10`
`=(2x+1)^2+10>=10`
Dấu "=" xảy ra khi `x=-1/2`
`C=(x-1)(x+3)(x+2)(x+6)`
`=[(x-1)(x+6)][(x+3)(x+2)]`
`=(x^2+5x-6)(x^2+5x+6)`
`=(x^2+5x)^2-36>=-36`
Dấu "=" xảy ra khi `x=0\or\x=-5`
`D=5-8x-x^2`
`=21-16-8x-x^2`
`=21-(x^2+8x+16)`
`=21-(x+4)^2<=21`
Dấu "=" xảy ra khi `x=-4`
`E=4x-x^2+1`
`=5-4+4-x^2`
`=5-(x^2-4x+4)`
`=5-(x-2)^2<=5`
Dấu "=" xảy ra khi `x=5`
7 tháng 10 2021
\(a,E=\dfrac{\sqrt{x}\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-1\right)^2}:\dfrac{x-1+\sqrt{x}+2-x}{\sqrt{x}\left(\sqrt{x}-1\right)}\left(x>0;x\ne1\right)\\ E=\dfrac{\sqrt{x}\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-1\right)^2}\cdot\dfrac{\sqrt{x}\left(\sqrt{x}-1\right)}{\sqrt{x}+1}=\dfrac{x}{\sqrt{x}-1}\\ b,E>1\Leftrightarrow\dfrac{x-\sqrt{x}+1}{\sqrt{x}-1}>0\\ \Leftrightarrow\sqrt{x}-1>0\left[x-\sqrt{x}+1=\left(\sqrt{x}-\dfrac{1}{2}\right)^2+\dfrac{3}{4}\ge\dfrac{3}{4}>0\right]\\ \Leftrightarrow x>1\left(tm\right)\)
\(c,E=\dfrac{x}{\sqrt{x}-1}=\dfrac{x-1+1}{\sqrt{x}-1}=\sqrt{x}+1+\dfrac{1}{\sqrt{x}-1}\\ E=\sqrt{x}-1+\dfrac{1}{\sqrt{x}-1}+2\ge2\sqrt{\dfrac{\sqrt{x}-1}{\sqrt{x}-1}}+2=2+2=4\\ E_{min}=4\Leftrightarrow\sqrt{x}-1=1\Leftrightarrow x=4\)
CM
27 tháng 9 2018
a) Rút gọn E Þ đpcm.
b) Điều kiện xác định E là: x ≠ ± 1
Rút gọn F ta thu được F = 4 Þ đpcm
8 tháng 3 2016
a)\(\frac{1+\left(1+2\right)+\left(1+2+3\right)+...+\left(1+2+3+...+98\right)}{1.98+2.97+3.96+....+98.1}\)
\(=\frac{\left(1+1+....+1\right)+\left(2+2+...2\right)+....+\left(97+97\right)+98}{ }\)
\(=\frac{1.98+2.97+3.96+....+97.2+98.1}{1.98+2.97+3.96+....+98.1}=1\)
CM
5 tháng 3 2018
Chọn C
Gọi A (d; e; f) thì A thuộc mặt cầu (S1): (x - 1)2 + (y - 2)2 + (z- 3)2 = 1 có tâm I1 = (1; 2; 3), bán kính R1 = 1
B (a; b; c) thì B thuộc mặt cầu (S2): (x - 3)2 + (y - 2)2 + z2 = 9 có tâm I2 = (-3; 2; 0), bán kính R2 = 3
Ta có I1I2 = 5 > R1 + R2 => (S1) và (S2) không cắt nhau và ở ngoài nhau.
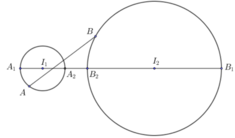
Dễ thấy F = AB, AB max khi A ≡ A1; B ≡ B1
=> Giá trị lớn nhất bằng I1I2 + R1 + R2 = 9.
AB min khi A ≡ A2; B ≡ B2
=> Giá trị nhỏ nhất bằng I1I2 - R1 - R2 = 1.
Vậy M - m =8
Đáp án : B