Gọi m 0 là giá trị của tham số m để đường thẳng đi qua điểm cực đại và cực tiểu của đồ thị hàm số y = x 3 - 6 m x + 4 cắt đường tròn tâm I(1;0), bán kính bằng 2 tại hai điểm phân biệt A, B sao cho diện tích tam giác IAB đạt giá trị lớn nhất. Mệnh đề nào sau đây đúng:
![]()
![]()
![]()
![]()

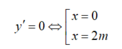
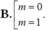
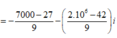
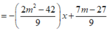

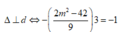
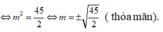
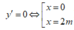
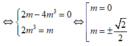





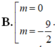

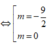
Chọn C