Cho đường tròn (C) có tâm I, bán kính R = a . Gọi M là điểm nằm ngoài (C) và I M = a 3 ; A là điểm thuộc (C) và MA tiếp xúc với (C); H là hình chiếu của A trên đường thẳng IM. Tính theo a thể tích V của khối tròn xoay tạo bởi hình tam giác MAH quay xung quanh trục IM
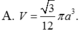
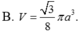
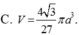
![]()

